Interpretasi Fisik
Interpretasi Fisik. Dalam dua bagian sebelumnya, kita mengembangkan persamaan dasar yang mengatur gerakan fluida di bawah serangkaian pembatasan yang cukup ketat. Meskipun banyak asumsi yang diberlakukan pada aliran ini, berbagai aliran dapat dengan mudah dianalisis dengan menggunakan persamaan ini. Interpretasi fisik dari persamaan tersebut akan membantu dalam memahami proses yang terlibat. Dengan tujuan ini, kita menulis kembali Persamaan 3.7 dan 3.12 di sini dan menginterpretasikannya secara fisik. Penerapan F=ma sepanjang dan normal terhadap garis aliran menghasilkan:

Dan
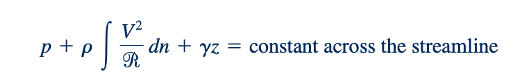
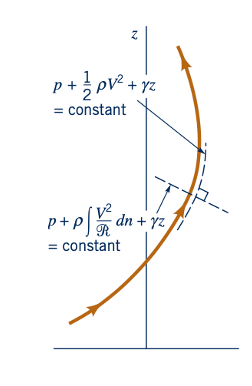
seperti yang ditunjukkan oleh gambar di pinggir halaman.
Berikut adalah asumsi dasar yang dibuat untuk mendapatkan persamaan-persamaan ini: Aliran adalah stabil, dan fluida tidak viskos dan tidak dapat dimampatkan. Dalam praktiknya, tidak satu pun dari asumsi ini secara tepat benar. Pelanggaran salah satu atau lebih dari asumsi di atas adalah penyebab umum ketidakcocokan antara " dunia nyata " dan solusi yang diperoleh dengan menggunakan persamaan Bernoulli. Untungnya, banyak situasi " dunia nyata " dapat dimodelkan dengan baik dengan menggunakan Pers. 3.13 dan 3.14 karena aliran hampir stabil dan tidak dapat dimampatkan serta fluida bersifat hampir tak ber-viskos.
Persamaan Bernoulli diperoleh dengan mengintegrasikan persamaan gerak sepanjang arah koordinat " alami " dari garis aliran.
Untuk menghasilkan percepatan, harus ada ketidakseimbangan gaya resultant, di mana hanya tekanan dan gravitasi yang dianggap penting. Dengan demikian,
Ada tiga proses yang terlibat dalam aliran - massa kali percepatan (term pV2/2), tekanan (term p), dan berat (term 𝛾z).
Integrasi persamaan gerak untuk memberikan Pers. 3.13 sebenarnya sesuai dengan prinsip kerja-energi yang sering digunakan dalam studi dinamika [lihat teks dinamika standar apa pun]. Prinsip ini berasal dari integrasi umum persamaan gerak untuk sebuah objek dengan cara yang sangat mirip dengan yang dilakukan untuk partikel fluida di Bagian 3.2. Dengan asumsi tertentu, pernyataan prinsip kerja-energi dapat ditulis sebagai berikut: Kerja yang dilakukan pada sebuah partikel oleh semua gaya yang bekerja pada partikel tersebut sama dengan perubahan energi kinetik partikel tersebut.
Persamaan Bernoulli adalah pernyataan matematis dari prinsip ini. Saat partikel fluida bergerak, baik gaya gravitasi maupun tekanan melakukan kerja pada partikel tersebut. Ingatlah bahwa kerja yang dilakukan oleh suatu gaya sama dengan hasil kali jarak yang ditempuh oleh partikel tersebut dengan komponen gaya dalam arah perjalanan (yaitu, kerja sama dengan F kali d). Istilah 𝛾z dan p dalam Pers. 3.13 berkaitan dengan kerja yang dilakukan oleh gaya berat dan gaya tekanan, masing-masing.
Sementara itu, term yang tersisa, yaitu pV2/2, jelas berkaitan dengan energi kinetik partikel. Bahkan, metode alternatif untuk mendapatkan persamaan Bernoulli adalah dengan membagi setiap term dari Pers. 3.7 dengan berat jenis, 𝛾, untuk memperoleh

Setiap istilah dalam persamaan ini memiliki satuan energi per berat (LF/F=L) atau (panjang dalam kaki, meter) dan mewakili jenis head tertentu.
Istilah elevasi, z, berkaitan dengan energi potensial partikel dan disebut head elevasi. Istilah tekanan, p/𝛾, disebut head tekanan dan mewakili tinggi kolom cairan yang diperlukan untuk menghasilkan tekanan p. Istilah kecepatan, V²/2g, adalah head kecepatan dan mewakili jarak vertikal yang diperlukan bagi cairan untuk jatuh secara bebas (mengabaikan gesekan) jika mencapai kecepatan V dari keadaan diam. Persamaan Bernoulli menyatakan bahwa jumlah head tekanan, head kecepatan, dan head elevasi adalah konstan sepanjang suatu streamline.
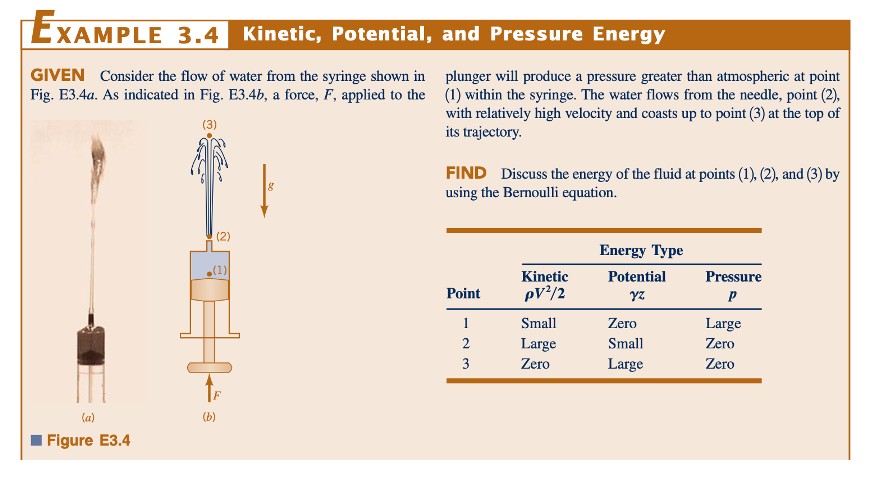

Sebuah gaya bersih diperlukan untuk mempercepat massa apa pun. Untuk aliran yang stabil, percepatan dapat diinterpretasikan sebagai muncul dari dua kejadian yang berbeda – perubahan kecepatan sepanjang streamline dan perubahan arah jika streamline tidak lurus. Integrasi persamaan gerak sepanjang streamline memperhitungkan perubahan kecepatan (perubahan energi kinetik) dan menghasilkan persamaan Bernoulli. Integrasi persamaan gerak tegak lurus terhadap streamline memperhitungkan percepatan sentrifugal (V2/R) dan menghasilkan Persamaan 3.14.
Ketika sebuah partikel fluida bergerak sepanjang jalur melengkung, suatu gaya bersih yang mengarah ke pusat kelengkungan diperlukan. Di bawah asumsi yang berlaku untuk Persamaan 3.14, gaya ini mungkin merupakan gaya gravitasi atau tekanan, atau kombinasi keduanya. Dalam banyak kasus, garis aliran hampir lurus (r ≈ ∞), sehingga efek sentrifugal dapat diabaikan dan variasi tekanan sepanjang garis aliran hanyalah hidrostatik (karena gravitasi saja), meskipun fluida bergerak.