10.2.14 Algoritma Matriks Pentadiagonal (PDMA)
Algoritma Matriks PentaDiagonal (PDMA) [7–10], menyelesaikan sistem persamaan aljabar dengan matriks koefisien pentadiagonal yang timbul dari skema diskritisasi yang menghubungkan nilai pada titik grid i dengan nilai-nilai dua titik di hulu (i − 1 dan i − 2) dan dua titik di hilir (i + 1 dan i + 2) yang berdekatan. Untuk notasi yang diilustrasikan secara skematis dalam Gambar 10.1, persamaan aljabar umum ditulis sebagai berikut
tergantung pada
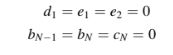
Untuk i = 1, Pers. (10.37) memberikan
Sementara untuk i = 2, nilai dari ditemukan
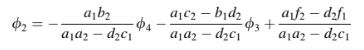
Proses ini dapat dilanjutkan untuk nilai i lainnya, dan secara umum, dapat diungkapkan sebagai
Menghitung dan
menggunakan Pers. (10.41) dan menggantikan nilainya dalam Pers. (10.37), suatu persamaan untuk
dapat diperoleh
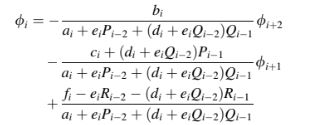
Dengan membandingkan Pers. (10.41) dan (10.42), Pi, Qi, dan Ri ditemukan sebagai
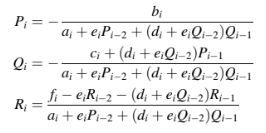
dengan nilai mereka untuk i = 1 dan 2 yang diberikan oleh
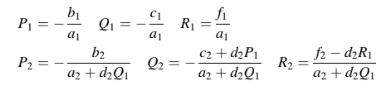
Karenamaka
Dengan demikian, persamaan untuk
dan
ditemukan dari
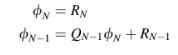
Algoritma solusi PDMA dapat disajikan sebagai berikut:

