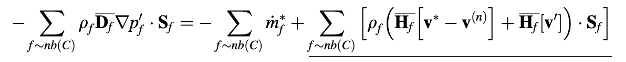Algoritma PRIME
Dalam algoritma PRIME (PRessure Implicit Momentum Explicit) [19], persamaan momentum diselesaikan secara eksplisit. Perlakuan eksplisit ini dibenarkan oleh kontribusi kecil terhadap konvergensi medan aliran keseluruhan oleh penyelesaian iteratif persamaan momentum. Di sisi lain, menemukan solusi yang benar untuk medan tekanan merupakan faktor paling penting dalam konvergensi keseluruhan. Berdasarkan argumen ini, algoritma PRIME dapat dirangkum sebagai berikut:
Persamaan momentum diselesaikan secara eksplisit untuk memperoleh medan kecepatan baru v* menggunakan
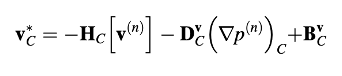
Medan kecepatan ini digunakan untuk menurunkan persamaan koreksi tekanan. Dengan demikian, mendefinisikan medan koreksi sehingga
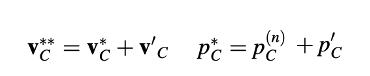
medan yang diperbaiki akan memenuhi
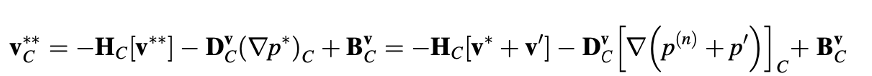
mengarah pada ekspresi berikut yang menghubungkan koreksi kecepatan dan tekanan:
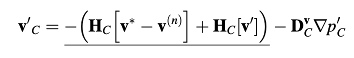
Menggantikan Persamaan (15.179) dan koreksinya ke dalam persamaan kontinuitas menghasilkan