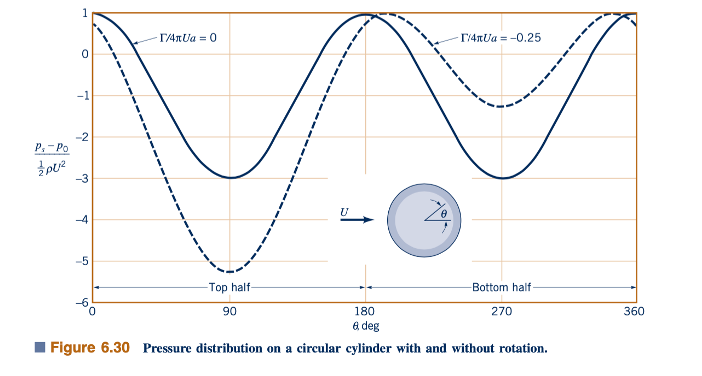
Aliran di sekitar Silinder Melingkar
Aliran di sekitar silinder melingkar. Seperti yang dicatat dalam bagian sebelumnya, ketika jarak antara pasangan sumber-sumuran mendekati nol, bentuk oval Rankine menjadi lebih tumpul dan sebenarnya mendekati bentuk lingkaran. Karena doublet yang dijelaskan dalam Bagian 6.5.4 dikembangkan dengan membiarkan pasangan sumber-sumuran mendekati satu sama lain, diharapkan bahwa aliran seragam dalam arah positif sumbu x yang dikombinasikan dengan doublet dapat digunakan untuk merepresentasikan aliran di sekitar silinder lingkaran. Kombinasi ini memberikan untuk fungsi aliran

dan untuk potensi kecepatan

Untuk membuat fungsi aliran mewakili aliran di sekitar silinder lingkaran, penting bahwa 𝜓 = konstan untuk r = a, di mana a adalah jari-jari silinder. Karena Persamaan 6.110 dapat ditulis sebagai

maka 𝜓 = 0 untuk r = a jika

yang mengindikasikan bahwa kekuatan doublet, K, harus sama dengan Ua2 . Dengan demikian, fungsi aliran untuk aliran di sekitar sebuah silinder lingkaran dapat dinyatakan sebagai

dan potensial kecepatan yang sesuai adalah

Suatu sketsa dari garis aliran untuk medan aliran ini ditunjukkan dalam Gambar 6.26.
Komponen kecepatan dapat diperoleh dari Persamaan 6.112 atau 6.113 sebagai

Dan

Pada permukaan silinder (r=a ), maka dari Persamaan 6.114 dan 6.115, kita memiliki vr =0 dan

Seperti yang ditunjukkan oleh gambar di pinggir, kecepatan maksimum terjadi di bagian atas dan bawah silinder (𝜃= ± /2π) dan memiliki magnitudo dua kali lipat dari kecepatan hulu, U. Saat kita menjauh dari silinder sepanjang garis 𝜃= π/2 , kecepatan bervariasi, seperti yang diilustrasikan dalam Gambar 6.26.

Distribusi tekanan pada permukaan silinder diperoleh dari persamaan Bernoulli yang dituliskan dari suatu titik yang jauh dari silinder di mana tekanannya adalah p0 dan kecepatannya adalah U sehingga

di mana ps adalah tekanan permukaan. Perubahan ketinggian diabaikan. Karena V𝜃u=-2 U sin𝜃 , tekanan permukaan dapat diekspresikan sebagai

Sebuah perbandingan distribusi tekanan teoritis, simetris yang diekspresikan dalam bentuk tak berdimensi dengan distribusi yang diukur secara tipikal ditunjukkan dalam Gambar 6.27. Gambar ini dengan jelas mengungkapkan bahwa hanya pada bagian hulu dari silinder terdapat kesesuaian yang mendekati antara aliran potensial dan hasil eksperimen. Karena lapisan batas viskos yang berkembang di sekitar silinder, aliran utama terpisah dari permukaan silinder, menyebabkan perbedaan besar antara solusi teoritis, fluida yang bebas gesekan, dan hasil eksperimen di sisi hilir dari silinder.
Gaya resultan (per satuan panjang) yang terbentuk pada silinder dapat ditentukan dengan mengintegrasikan tekanan di atas permukaan. Dari Gambar 6.28 dapat terlihat bahwa.



Di mana Fx adalah gaya gesekan (force) (sejajar dengan arah aliran seragam) dan Fy adalah gaya angkat (force) (tegak lurus terhadap arah aliran seragam). Penggantian untuk p dari Persamaan 6.116 ke dalam kedua persamaan ini, dan integrasi berikutnya, mengungkapkan bahwa Fx =0 dan Fy =0. Hasil ini menunjukkan bahwa baik gaya gesekan maupun gaya angkat seperti yang diprediksi oleh teori potensial untuk sebuah silinder tetap dalam aliran seragam adalah nol. Karena distribusi tekanan bersifat simetris di sekitar silinder, ini bukanlah hasil yang mengejutkan. Namun, kita tahu dari pengalaman bahwa ada gaya gesekan yang signifikan yang terjadi pada sebuah silinder ketika ditempatkan dalam fluida yang bergerak. Diskrepansi ini dikenal sebagai paradoks d'Alembert. Paradoks ini dinamai dari Jean le Rond d'Alembert (1717–1783), seorang matematikawan dan filsuf Prancis, yang pertama kali menunjukkan bahwa gaya gesekan pada benda yang terendam dalam fluida yang tak kental adalah nol. Baru pada akhir abad kesembilan belas dan awal abad kedua puluh pemahaman tentang peran viskositas dalam gerakan fluida yang stabil dipahami dan paradoks d'Alembert dijelaskan.


Sebuah aliran potensial tambahan dan menarik dapat dikembangkan dengan menambahkan pusaran bebas (free vortex) ke dalam fungsi aliran atau potensial kecepatan untuk aliran di sekitar sebuah silinder. Dalam kasus inI
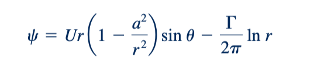
Dan

dimana Γ adalah sirkulasi. kita perhatikan bahwa r=a akan tetap menjadi garis arus (dan dengan demikian dapat diganti dengan silinder padat), karena garis arus untuk pusaran bebas yang ditambah semuanya berbentuk lingkaran. Namun kecepatan tangensial, Va pada permukaan silinder (ra) kini menjadi

Tipe medan aliran seperti ini dapat dibuat secara kasar dengan menempatkan sebuah silinder yang berputar dalam aliran seragam. Karena adanya viskositas dalam setiap fluida nyata, fluida yang bersentuhan dengan silinder yang berputar akan berputar dengan kecepatan yang sama dengan silinder, dan medan aliran yang dihasilkan akan menyerupai kombinasi aliran seragam melewati silinder dan pusaran bebas.

Berbagai pola garis aliran dapat dikembangkan,Γ. untuk tergantung pada kekuatan pusaran, misalnya, dari Persamaan 6.121 kita dapat menentukan lokasi titik stagnasi pada permukaan silinder. Titik-titik ini akan terjadi pada 𝜃 = 𝜃 stag di mana v𝜃=0 dan karena itu dari Persamaan 6.121

Jika Γ = 0, maka 𝜃u stag=0 atau π — yaitu, titik stagnasi terjadi di depan dan belakang silinder seperti yang ditunjukkan dalam Gambar 6.29a. Namun, untuk -1 ≤ Γ/ 4πUa ≤ 1 , titik stagnasi akan terjadi di lokasi lain pada permukaan seperti yang diilustrasikan dalam Gambar 6.29b,c. Jika nilai absolut dari parameter Γ/ 4πUa melebihi 1, Persamaan 6.122 tidak dapat dipenuhi, dan titik stagnasi terletak jauh dari silinder seperti yang ditunjukkan dalam Gambar 6.29d.
Gaya per satuan panjang yang terbentuk pada silinder dapat lagi diperoleh dengan mengintegrasikan gaya tekanan diferensial di sekeliling lingkarannya seperti dalam Persamaan 6.117 dan 6.118. Untuk silinder dengan sirkulasi, tekanan permukaan p diperoleh dari persamaan Bernoulli dengan kecepatan permukaannya yang diberikan oleh Persamaan 6.121.

Atau

Persamaan 6.123 digantikan ke dalam Persamaan 6.117 untuk gaya gesekan, dan diintegrasikan, kembali menghasilkan

Artinya, bahkan untuk silinder yang berputar, tidak ada gaya dalam arah aliran seragam yang terbentuk. Namun, penggunaan Persamaan 6.123 dengan persamaan untuk gaya angkat, Fy (Persamaan 6.118), menghasilkan
Dengan demikian, untuk silinder dengan sirkulasi, gaya angkat terbentuk sama dengan hasil kali antara densitas fluida, kecepatan hulu, dan sirkulasi. Tanda negatif berarti bahwa jika U positif (dalam arah x positif) dan sirkulasi positif (sebuah pusaran bebas dengan rotasi berlawanan arah jarum jam), arah darii Fy adalah ke bawah.
Tentu saja, jika silinder diputar dalam arah searah jarum jam (Γ>0), arah dari Fy akan ke atas. Hal ini dapat dilihat dengan mempelajari distribusi tekanan permukaan (Persamaan 6.123), yang digambarkan dalam Gambar 6.30 untuk dua situasi. Salah satunya memiliki Γ/ 4πUa =0, yang sesuai dengan tidak adanya rotasi silinder. Yang lain memiliki Γ/4πUa =−0.25, yang sesuai dengan rotasi searah jarum jam dari silinder.