Aliran Laminar dan Mantap antara Pelat Paralel Tetap
Aliran Laminar dan Mantap antara Pelat Paralel Tetap. Kita pertama-tama mempertimbangkan aliran antara dua plat paralel horizontal tak terbatas seperti pada Gambar 6.31a. Untuk geometri ini, partikel-fluida bergerak dalam arah x sejajar dengan plat, dan tidak ada kecepatan dalam arah y atau z — yaitu, v = 0 dan w = 0. Dalam hal ini, dari persamaan kontinuitas (Eq. 6.312) mengikuti bahwa ∂u/∂x = 0. Selain itu, tidak akan ada variasi u dalam arah z untuk plat yang tak terbatas, dan untuk aliran seimbang ∂u/∂t = 0 sehingga u = u(y). Jika kondisi ini digunakan dalam persamaan Navier-Stokes (Eqs. 6.127), maka reduksi menjadi
Yang merupakan bentuk yang disederhanakan dari persamaan Navier-Stokes untuk aliran antara dua plat paralel tak terbatas.
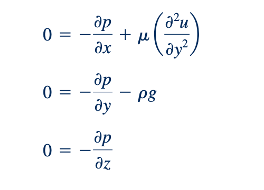
Kita telah menetapkan gx = 0, gy = -g, dan gz = 0. Artinya, sumbu y menunjuk ke atas. Kita melihat bahwa untuk masalah ini, persamaan Navier-Stokes menyederhanakan menjadi persamaan yang cukup sederhana.
Persamaan 6.130 dan 6.131 dapat diintegralkan untuk menghasilkan
menunjukkan bahwa tekanan bervariasi secara hidrostatik dalam arah y. Persamaan 6.129, ditulis ulang sebagai
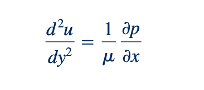
dapat diintegrasikan untuk memberikan

dan diintegrasikan lagi untuk memberikan

Perhatikan bahwa untuk aliran sederhana ini, gradien tekanan, ∂p/∂x , diperlakukan sebagai konstan sejauh integrasi yang bersangkutan, karena 1seperti yang ditunjukkan dalam Persamaan 6.1322 gradien tersebut tidak merupakan fungsi dari y. Konstan c1 dan c2 harus ditentukan dari kondisi batas. Sebagai contoh, jika dua pelat tersebut

tertentu, maka u =0 untuk y= ± ℎ (karena kondisi no-slip untuk fluida viskos). Untuk memenuhi kondisi ini, c1=0 dan

Oleh karena itu, distribusi kecepatan menjadi
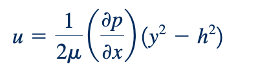
Persamaan 6.134 menunjukkan bahwa profil kecepatan antara dua pelat yang diam adalah parabola, seperti yang diilustrasikan di Gambar 6.31b.
Laju aliran volume, q, yang melewati antara dua pelat (untuk lebar satuan ke arah z) diperoleh dari hubungan

Atau

Gradien tekanan 𝜕𝑝/𝜕𝑥 adalah negatif, karena tekanan menurun ke arah aliran. Jika kita biarkan ∆𝑝 mewakili penurunan tekanan antara dua titik yang berjarak ℓ apart, maka

dan Persamaan 6.135 dapat diekspresikan sebagai:

Aliran berbanding lurus dengan gradien tekanan, berbanding terbalik dengan viskositas, dan sangat (-h) bergantung pada lebar celah. Dalam hal kecepatan rata-rata, V, di mana V = q / (2h), Persamaan 6.136 menjadi

Persamaan 6.136 dan 6.137 memberikan hubungan yang nyaman untuk menghubungkan penurunan tekanan sepanjang saluran plat-paralel dan laju aliran atau kecepatan rata-rata. Kecepatan maksimum, u_maks, terjadi di tengah-tengah (y = 0) antara dua plat, seperti yang ditunjukkan dalam Gambar 6.31b, sehingga dari Persamaan 6.134
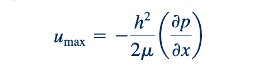
Atau
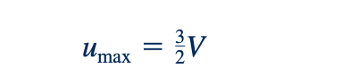
Detail dari aliran laminar stabil antara plat-paralel tak terhingga sepenuhnya diprediksi oleh solusi ini untuk persamaan Navier-Stokes. Misalnya, jika gradien tekanan, viskositas, dan jarak plat ditentukan, maka dari Persamaan 6.134 profil kecepatan dapat ditentukan, dan dari Persamaan 6.136 dan 6.137 laju aliran dan kecepatan rata-rata yang sesuai dapat ditentukan. Selain itu, karena gradien tekanan dalam arah x konstan, dari Persamaan 6.132 terjadi

di mana p0 adalah tekanan referensi saat x=y=0, dan variasi tekanan di seluruh fluida dapat diperoleh dari:

