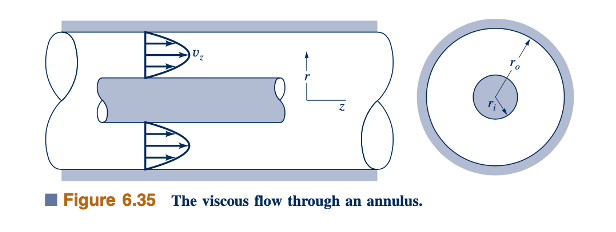
Aliran Laminar dan Mantap dalam Tabung Melingkar
Aliran laminar dan mantap dalam tabung melingkar. Mungkin solusi eksak yang paling terkenal untuk persamaan Navier-Stokes adalah untuk aliran laminar, tak dapat dipadatkan, stabil melalui tabung lingkaran lurus dengan penampang konstan. Jenis aliran ini umumnya disebut sebagai aliran Hagen-Poiseuille, atau hanya aliran Poiseuille. Nama ini diambil dari J. L. Poiseuille 11799–18692, seorang dokter Prancis, dan G. H. L. Hagen 11797–18842, seorang insinyur hidrolik Jerman. Poiseuille tertarik pada aliran darah melalui kapiler dan secara eksperimental menyimpulkan hukum resistansi untuk aliran laminar melalui tabung lingkaran. Penelitian Hagen tentang aliran dalam tabung juga bersifat eksperimental. Sebenarnya, setelah karya Hagen dan Poiseuille, hasil teoritis yang disajikan dalam bagian ini ditentukan, tetapi nama mereka umumnya dikaitkan dengan solusi masalah ini.
Berdasarkan geometri silinder, nyaman untuk menggunakan koordinat silinder. Kami mengasumsikan bahwa aliran sejajar dengan dinding sehingga vr = 0 dan v𝜃 = 0, dan dari persamaan kontinuitas 16.342 𝜕𝑣𝑧/𝜕𝑧 = 0. Juga, untuk aliran steady dan simetris terhadap sumbu, vz tidak merupakan fungsi dari t atau 𝜃, sehingga kecepatan, vz,
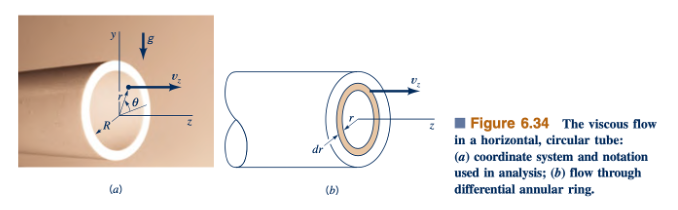
hanya merupakan fungsi dari posisi radial di dalam tabung — yaitu, vz = vz (r). Dalam kondisi ini, persamaan Navier–Stokes menjadi:
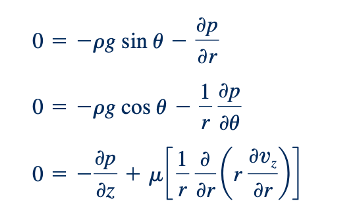
di mana kami telah menggunakan hubungan gr = - g sin 𝜃 dan g𝜃=-g cos 𝜃 (dengan 𝜃 diukur dari bidang horizontal).
Persamaan 6.143 dan 6.144 dapat diintegrasikan untuk memberikan
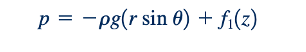
Atau
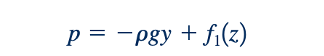
Persamaan 6.146 menunjukkan bahwa tekanan didistribusikan secara hidrostatik pada setiap penampang melintang, dan komponen z dari gradien tekanan, 𝜕𝑝/𝜕z, tidak bergantung pada r atau 𝜃.
Pada langkah ini, persamaan gerak dalam arah z (Eq. 6.145) dapat dituliskan dalam bentuk:
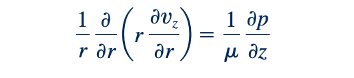
dan diintegralkan (dengan memanfaatkan fakta bahwa ∂p/∂z adalah konstan) menjadi:
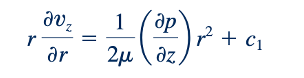
Diintegralkan lagi kita dapatkan:
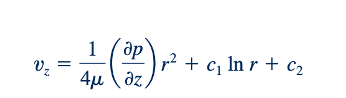
Seperti yang ditunjukkan oleh gambar di sisi margin, bentuk profil kecepatan tergantung pada nilai dari dua konstanta c1 dan c2.
Karena kita ingin vz tetap berhingga di tengah tabung (r=0), maka c1 = 0 karena ln (0) = −∞. Pada dinding (r=R) kecepatan harus nol sehingga.
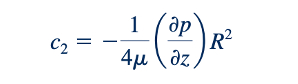
dan distribusi kecepatan menjadi
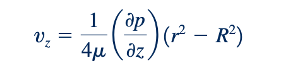
Oleh karena itu, pada setiap penampang, distribusi kecepatan adalah parabolik.
Untuk mendapatkan hubungan antara laju aliran volume, Q, yang melewati tabung dan gradien tekanan, kita pertimbangkan aliran melalui cincin berbentuk cuci, diferensial,Gambar 6.34b. Karena vz konstan pada cincin ini, laju aliran volume melalui luasan diferensial dA=(2𝜋r) adalah
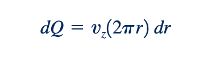
dan maka dari itu
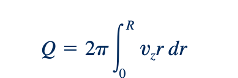
Persamaan 6.148 untuk vz dapat disubstitusikan ke dalam Persamaan 6.149, dan persamaan yang dihasilkan tersebut diintegrasikan untuk menghasilkan.
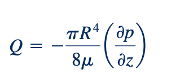
Hubungan ini dapat dinyatakan dalam istilah penurunan tekanan, ∆𝑝, yang terjadi selama sebuah panjang, ℓ, sepanjang tabung, karena
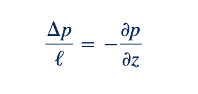
dan maka dari itu
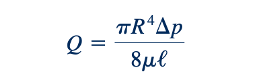
untuk suatu penurunan tekanan per satuan panjang yang diberikan, laju aliran volume berbanding terbalik dengan viskositas dan berbanding lurus dengan pangkat empat jari-jari tabung. Pembaruan jari-jari tabung menghasilkan peningkatan aliran 16 kali lipat! Persamaan 6.151 umumnya disebut hukum Poiseuille.
Dalam hal kecepatan rata-rata, V, di mana V = Q/𝜋R^2, Persamaan 6.151 menjadi
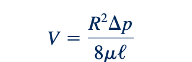
Kecepatan maksimum v max terjadi di tengah tabung, di mana dari Persamaan 6.148
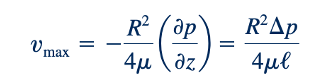
Sehingga
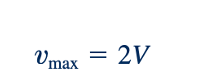
Distribusi kecepatan, seperti yang ditunjukkan oleh gambar di pinggir, dapat ditulis dalam istilah v max sebagai .
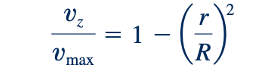
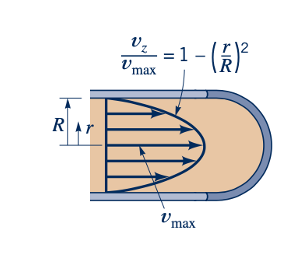
Seperti halnya untuk kasus serupa aliran antara plat paralel (terkadang disebut sebagai aliran Poiseuille datar), deskripsi yang sangat rinci tentang tekanan dan distribusi kecepatan dalam aliran tabung dihasilkan dari solusi ini terhadap persamaan Navier-Stokes. Sejumlah eksperimen yang dilakukan untuk menegaskan hasil teoritis menunjukkan bahwa teori dan eksperimen sejalan untuk aliran laminar dari fluida Newtonian dalam tabung atau pipa melingkar. Secara umum, aliran tetap laminar untuk nomor Reynolds, Re = pV(2R)/𝜇, di bawah 2100. Aliran turbulen dalam tabung dibahas di Bab 8.