
Chapter 5 Algoritma dan Penyelesaian
Chapter 5 Algoritma dan penyelesaian.
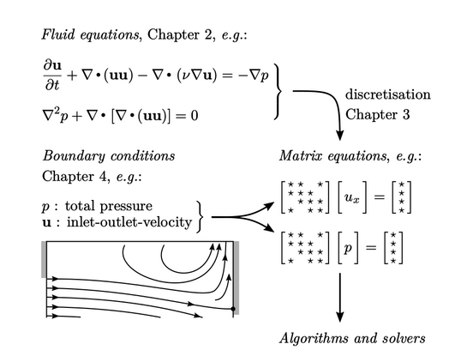
Bab-bab sebelumnya menjelaskan komponen-komponen yang diperlukan untuk membangun persamaan guna menyelesaikan masalah dalam dinamika fluida, yang tercantum di bawah ini:
- persamaan-persamaan pengaturan dan model-model umum, lihat Bab 2;
- metode numerik untuk membuat himpunan diskrit persamaan linear, sebagai persamaan matriks, lihat Bab 3;
- kondisi-kondisi batas, yang diterapkan pada persamaan-persamaan matriks, lihat Bab 4.
Komponen terakhir adalah merangkai himpunan persamaan matriks dan menerapkan algoritma untuk:
- menyelesaikan himpunan persamaan linear yang dijelaskan oleh setiap persamaan matriks individual;
- menggabungkan, atau mengkombinasikan, solusi dari beberapa persamaan matriks untuk menghasilkan solusi keseluruhan.
Bab ini pertama-tama membahas penyelesaian persamaan matriks individual. Ini menyajikan algoritma-algoritma paling efektif untuk menyelesaikan persamaan matriks yang dihadapi dengan metode volume terhingga.
Persyaratan penting dari solver matriks ini adalah kekokohan dan efisiensi, terutama untuk simulasi besar dengan jutaan sel. Solver yang menyertai metode volume terhingga umumnya bersifat iteratif, di mana solusinya konvergen ke tingkat akurasi atau toleransi yang diinginkan selama beberapa iterasi.
Algoritma-algoritma utama yang menggabungkan himpunan persamaan matriks kemudian akan disajikan. Penggabungan konservasi massa dan momentum dengan persamaan untuk u dan p adalah tantangan, dan oleh karena itu memerlukan perhatian khusus.
