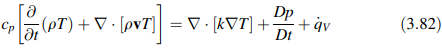CONSERVATION OF ENERGY IN TERMS OF TEMPERATURE
Conservation of energy in terms of temperature. Untuk dapat menulis persamaan energi dengan suhu sebagai variabel utama, beberapa batasan harus diberlakukan. Dengan mengasumsikan ℎ^h^ sebagai fungsi dari �p dan �T, diperkirakan bahwa fluida adalah Newtonian. Oleh karena itu, turunan yang akan dijelaskan berlaku hanya untuk fluida Newtonian. Jika ℎ^=ℎ^(�,�)h^=h^(p,T), maka �ℎ^dh^ dapat ditulis sebagai
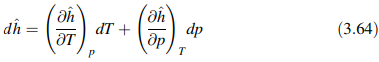
Dengan menggunakan hubungan termodinamika keseimbangan biasa berikut:
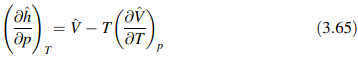
di mana V^ adalah volume spesifik, ekspresi untuk dh^ dapat dimodifikasi menjadi
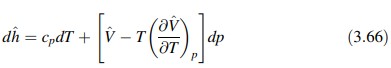
Bagian kiri entalpi spesifik [Persamaan (3.61)], dengan dh^ diberikan oleh Persamaan (3.66), dapat ditulis ulang dalam hal T sebagai
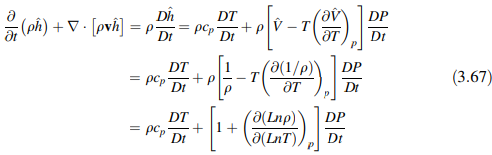
Dengan mensubstitusikan Persamaan (3.67) ke dalam Persamaan (3.61) memberikan persamaan energi dengan T sebagai variabel utamanya sebagai
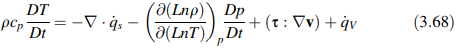
Persamaan di atas juga dapat dinyatakan sebagai
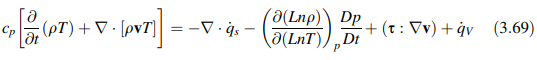
Fluks panas qS yang muncul dalam semua bentuk persamaan energi mewakili transfer panas oleh difusi, yang merupakan fenomena yang terjadi pada tingkat molekuler dan diatur oleh hukum Fourier menurut
di mana k adalah konduktivitas termal zat tersebut. Persamaan di atas menyatakan bahwa panas mengalir dalam arah gradien suhu dan mengasumsikan bahwa material tidak memiliki arah yang disukai untuk transfer panas dengan konduktivitas termal yang sama dalam semua arah, yaitu, medium tersebut adalah isotropik. Namun beberapa padatan adalah anisotropik di mana Persamaan (3.70) digantikan oleh
di mana j adalah tensor simetris orde kedua yang disebut tensor konduktivitas termal. Akibatnya, fluks panas dalam medium anisotropik tidak berada dalam arah gradien suhu. Dalam turunan yang akan datang, diasumsikan bahwa medium adalah isotropik dan Persamaan (3.70) berlaku. Menggantikan qS menggunakan hukum Fourier, persamaan energi, Persamaan (3.69), menjadi
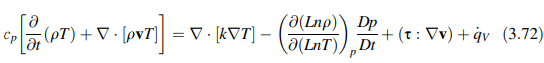
Ekspresi untuk dalam hal variabel aliran dalam sistem koordinat kartesian tiga dimensi diberikan oleh
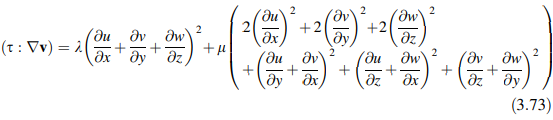
Mendefinisikan sebagai
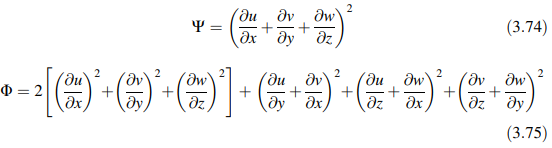
Persamaan energi dalam hal suhu menyederhanakan menjadi
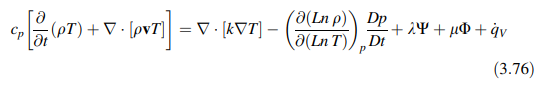
Untuk referensi selanjutnya, persamaan energi diperluas menjadi
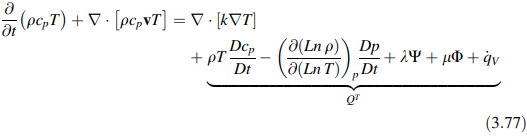
dan ditulis ulang sebagai
Persamaan energi jarang diselesaikan dalam bentuk lengkapnya, dan bergantung pada situasi fisik, beberapa versi yang disederhanakan dapat dikembangkan. Istilah disipasi Φ memiliki nilai yang dapat diabaikan kecuali untuk gradien kecepatan besar pada kecepatan supersonik. Selain itu, untuk fluida tak dapat dikompresi, persamaan kontinuitas menyiratkan bahwa �=0W=0 dan karena densitas konstan, ini mengikuti bahwa
Oleh karena itu, persamaan energi [Persamaan (3.77)] untuk aliran fluida tak dapat dikompresi disederhanakan menjadi
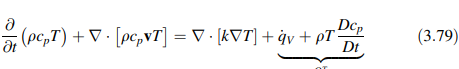
Persamaan (3.79) juga berlaku untuk fluida yang mengalir dalam sistem tekanan konstan. Untuk kasus padat, densitasnya konstan, kecepatannya nol, dan jika perubahan suhu tidak besar maka konduktivitas termal dapat dianggap konstan, dalam hal ini persamaan energi menjadi
Untuk gas ideal, persamaannya menjadi:
dan persamaan energi untuk aliran gas ideal dapat disederhanakan menjadi
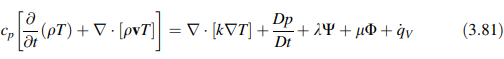
Jika viskositas diabaikan (artinya aliran adalah inviskid), Persamaan (3.81) lebih disederhanakan menjadi