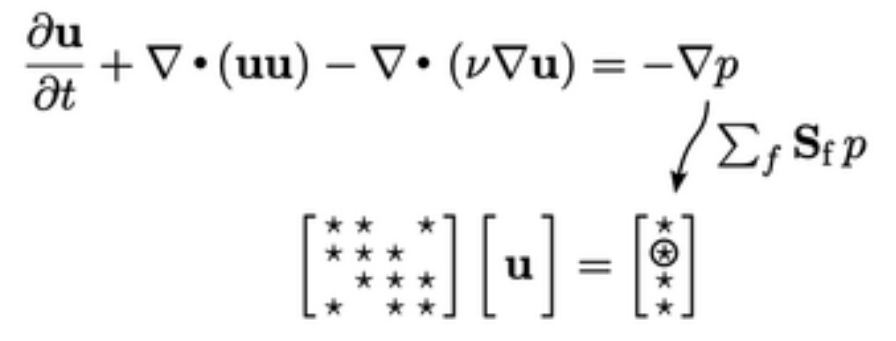CONTOH PEMBENTUKAN SUATU PERSAMAAN MATRIKS

Contoh pembentukan suatu persamaan matriks. Bagian-bagian sebelumnya menjelaskan metode-metode untuk mendiskritisasi turunan dan istilah-istilah lainnya untuk membangun suatu persamaan matriks untuk suatu persamaan fisika tertentu. Mari kita tunjukkan pembentukan suatu persamaan matriks, menggunakan persamaan konservasi momentum dari Bagian 3.23 sebagai contoh. Ini adalah suatu persamaan vektor, sehingga menghasilkan 3 persamaan matriks untuk 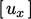, 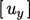dan .

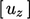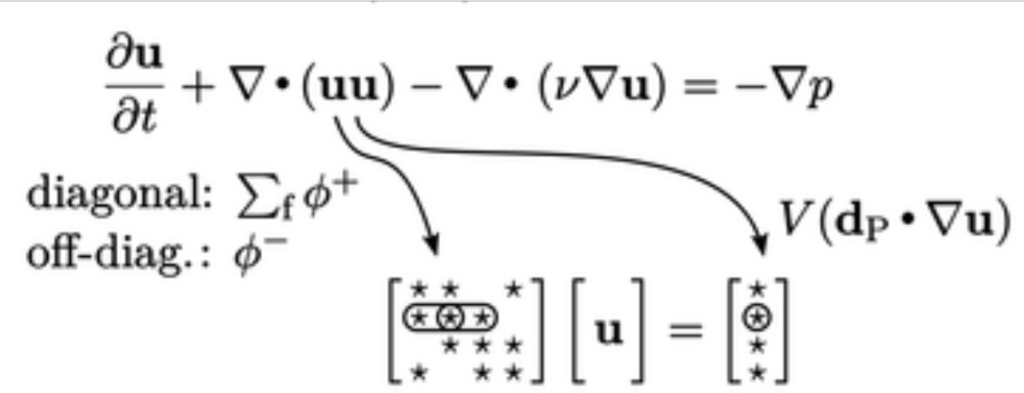
Istilah pertama, turunan waktu 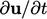, mungkin didiskritisasi dengan skema Euler persamaan (3.21). Persamaan matriks dibangun dalam bentuk ekstensif sebagaimana dibahas dalam bagian 3.6. Oleh karena itu, konstribusi dari persamaan (3.21) untuk koefisien matriks 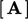dan vektor sumber 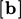diskalakan dengan volume sel 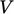, yaitu 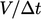dan 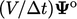, masing-masing, seperti yang diilustrasikan dibawah ini.

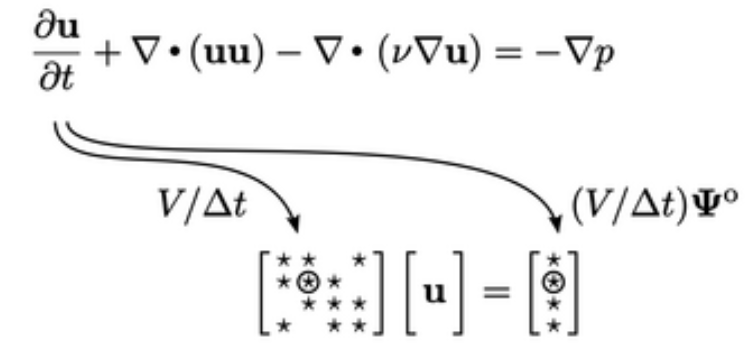
Istilah kedua, turunan adveksi 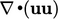, didiskritisasi oleh persamaan (3.8). Ini melakukan perhitungan pra-volume 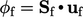, menggunakan 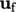yang diinterpolasi oleh persamaan (3.3) dengan bobot linear persamaan (3.4).

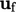yang diangkut mungkin didiskritisasi menggunakan skema upwind linier yang dijelaskan di bagian 3.14. Skema ini pertama-tama menerapkan diskritisasi upwind, yang memberikan kontribusi aliran positif keluar 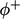ke koefisien diagonal dan aliran negatif 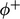ke luar diagonal. Kemudian, skema menambahkan kontribusi eksplisit berdasarkan gradien yang diekstrapolasi 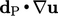(lihat bagian 3.14). Gradien 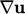biasanya dihitung dengan persamaan (3.18) dengan pembatasan gradien dari bagian 3.16.

Istilah ketga, turunan Laplace 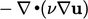, didiskritisasi oleh persamaan (3.2). Ini memerlukan 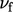, yang diinterpolasi secara linear dari pusat sel. Jika gradien normal permukaan 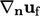termasuk koreksi non-ortogonal 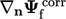, lihat bagian 3.8, maka istilah tersebut memberikan kontribusi pada 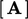dan 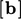, seperti yang ditunjukkan di bawah ini.

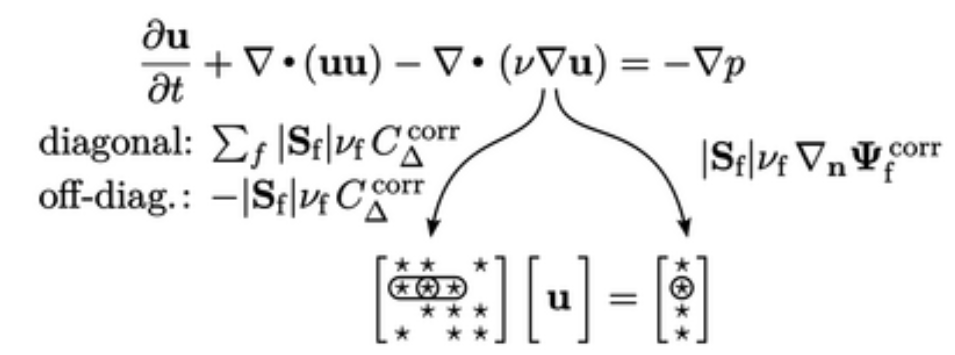
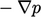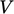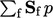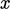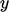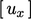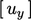Istilah terakhir, dihitung menggunakan persamaan (3.18). Seperti semua istilah lain yang dijelaskan di sini, itu diimplementasikan dalam bentuk ekstensif, diskalakan oleh , sehingga dihitung untuk setiap sel oleh vektor . Komponen yang relevan (, , ) dari vektor ini kemudian diterapkan pada persamaan masing-masing untuk , dan 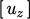.