Deskripsi Aliran Euler dan Lagrangian. Ada dua pendekatan umum dalam menganalisis masalah mekanika fluida (atau masalah dalam cabang ilmu fisika lainnya, pada dasarnya). Metode pertama, yang disebut metode Eulerian, menggunakan konsep lapangan yang diperkenalkan di atas. Dalam hal ini, gerakan fluida diberikan dengan sepenuhnya menentukan sifat-sifat yang diperlukan (tekanan, densitas, kecepatan, dll.) sebagai fungsi waktu dan ruang. Dari metode ini kita memperoleh informasi tentang aliran dalam hal apa yang terjadi pada titik-titik tetap dalam ruang ketika fluida mengalir melalui titik-titik tersebut.

Representasi Eulerian yang khas dari aliran ditunjukkan oleh gambar di pinggiran yang melibatkan aliran di sekitar airfoil dengan sudut serang. Medan tekanan ditunjukkan dengan menggunakan plot kontur yang menunjukkan garis-garis tekanan konstan, dengan bayangan abu-abu menunjukkan intensitas tekanan.

Metode kedua, yang disebut metode Lagrangian, melibatkan mengikuti partikel fluida individual saat mereka bergerak dan menentukan bagaimana sifat-sifat fluida yang terkait dengan partikel-partikel ini berubah sebagai fungsi waktu. Artinya, partikel-fluida "ditandai" atau diidentifikasi, dan sifat-sifat mereka ditentukan saat mereka bergerak.

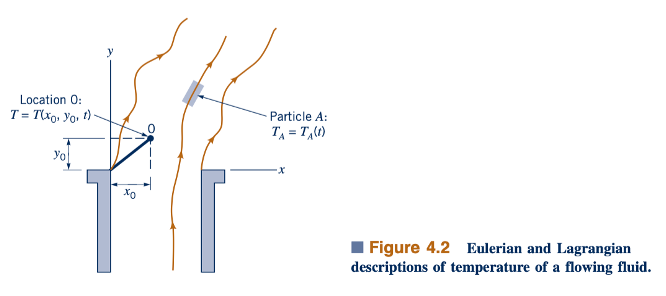
Perbedaan antara kedua metode dalam menganalisis masalah aliran fluida dapat dilihat dalam contoh asap yang keluar dari cerobong asap, seperti yang ditunjukkan pada Gambar 4.2. Dalam metode Eulerian, seseorang dapat melekatkan perangkat pengukur suhu di bagian atas cerobong asap (titik 0) dan mencatat suhu di titik tersebut sebagai fungsi waktu. Pada waktu yang berbeda, ada partikel-fluida yang berbeda melewati perangkat diam tersebut. Dengan demikian, seseorang akan memperoleh suhu, T, untuk lokasi tersebut (x = x0, y = y0, dan z = z0) sebagai fungsi waktu. Artinya, T = T(x0, y0, z0, t). Penggunaan banyak perangkat pengukur suhu yang dipasang di berbagai lokasi akan memberikan medan suhu, T = T(x, y, z, t). Suhu partikel sebagai fungsi waktu tidak akan diketahui kecuali lokasi partikel diketahui sebagai fungsi waktu.

Metode Lagrangian, seseorang akan melekatkan perangkat pengukur suhu pada suatu partikel fluida tertentu (partikel A) dan mencatat suhu partikel tersebut saat bergerak. Dengan demikian, seseorang akan memperoleh suhu partikel tersebut sebagai fungsi waktu, TA = TA(t). Penggunaan banyak perangkat pengukur semacam itu yang bergerak dengan berbagai partikel fluida akan memberikan suhu partikel-fluida tersebut sebagai fungsi waktu. Suhu tidak akan diketahui sebagai fungsi posisi kecuali lokasi setiap partikel diketahui sebagai fungsi waktu. Jika cukup banyak informasi dalam bentuk Eulerian tersedia, informasi Lagrangian dapat diperoleh dari data Eulerian—dan sebaliknya.

Contoh 4.1 memberikan deskripsi Eulerian dari aliran. Untuk deskripsi Lagrangian, kita perlu menentukan kecepatan sebagai fungsi waktu untuk setiap partikel saat mengalir dari satu titik ke titik lain.

Dalam mekanika fluida, biasanya lebih mudah menggunakan metode Eulerian untuk menjelaskan aliran—baik dalam investigasi eksperimental maupun analitis. Namun, ada beberapa kasus di mana metode Lagrangian lebih nyaman. Sebagai contoh, beberapa perhitungan mekanika fluida numerik didasarkan pada penentuan gerak partikel fluida individual (berdasarkan interaksi yang sesuai antara partikel-partikel tersebut), sehingga menjelaskan gerakan dalam istilah Lagrangian. Demikian pula, dalam