Efek Tak Stabil
Efek Tak Stabil. Pertimbangkan aliran yang tidak stabil (∂( )/∂t ≠ 0) sehingga semua istilah dalam Persamaan 4.19 harus dipertahankan. Ketika dilihat dari sudut pandang volume kontrol, jumlah parameter B dalam sistem dapat berubah karena jumlah B dalam volume kontrol tetap dapat berubah seiring waktu.
Karena ada kemungkinan bahwa jumlah parameter tersebut dapat berubah seiring waktu (term ∂ ∫cv pb d∀ /∂t) dan karena mungkin ada aliran bersih yang tidak nol dari parameter tersebut melintasi permukaan kontrol (term ∫ cs (pbV⋅n) dA).
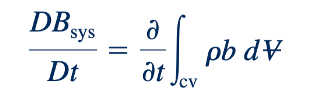
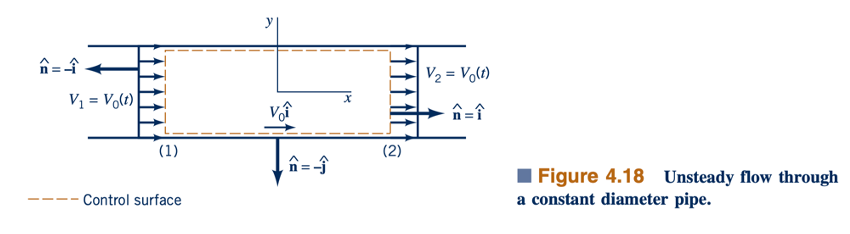
Untuk kasus seperti itu, setiap laju perubahan dalam jumlah B yang terkait dengan sistem sama dengan laju perubahan B dalam volume kontrol. Ini dapat diilustrasikan dengan mempertimbangkan aliran melalui pipa berdiameter konstan seperti yang ditunjukkan dalam Gambar 4.18. Volume kontrol adalah seperti yang ditunjukkan, dan sistem adalah fluida dalam volume ini pada waktu t0. Kami mengasumsikan aliran satu dimensi dengan V=V0 i^ , di mana V0(t) adalah fungsi waktu, dan bahwa densitasnya konstan. Pada setiap saat, semua partikel dalam sistem memiliki kecepatan yang sama. Kami membiarkan B= menjadi momentum sistem, yaitu mV = mV0 i^ , di mana m adalah massa sistem, sehingga b= m/B=V= V0i^ , kecepatan fluida. Besarnya efflux momentum melintasi keluaran [bagian (2)] sama dengan besarnya influx momentum melintasi masuk [bagian (1)]. Namun, tanda efflux berlawanan dengan tanda influx karena V⋅n > 0 untuk aliran keluar dan V⋅n < 0 untuk aliran masuk. Perhatikan bahwa V⋅n = 0 di sisi-sisi volume kontrol. Dengan demikian, dengan V⋅n=V0 di bagian (1), V⋅n=−V0 di bagian (2), dan A1 =A2, kita dapatkan
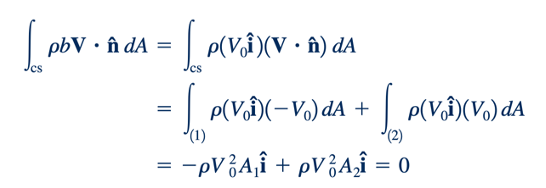
Dapat dilihat bahwa untuk kasus khusus ini Persamaan 4.21 berlaku. Laju perubahan momentum sistem dengan waktu sama dengan laju perubahan momentum dalam volume kontrol. Jika V0 konstan seiring waktu, tidak ada laju perubahan momentum sistem, dan untuk kasus khusus ini masing-masing dari istilah dalam teorema transportasi Reynolds adalah nol secara sendiri-sendiri.
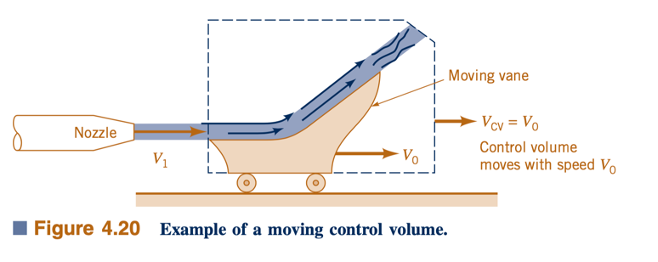
Pertimbangkan aliran melalui pipa dengan area variabel seperti yang ditunjukkan dalam Gambar 4.19. Dalam kasus seperti itu, kecepatan fluida tidak sama di bagian (1) dengan di bagian (2). Oleh karena itu, efflux momentum dari volume kontrol tidak sama dengan influx momentum, sehingga istilah konvektif dalam Persamaan 4.20 [integral dari ρV(V⋅n) di atas permukaan kontrol] tidak nol. Topik-topik ini akan dibahas dengan lebih detail dalam Bab 5.