flow THROUGH a surface
Flow Through a Surface. Konsep aliran melalui suatu permukaan muncul dalam banyak area pada konteks CFD, termasuk dalam persamaan dinamika fluida, metode numerik, kondisi batas, dan perhitungan aliran umum. Ketika kita berbicara tentang sesuatu yang melewati suatu permukaan, istilah fluks sering digunakan.
Untuk mengkauntifikasi fluks dari suatu properti, kita mengalikan luas permukaan dengan properti di permukaan tersebut. Jika properti tersebut adalah sebuah vektor, kita mengambil komponen yang normal terhadap permukaan. Sebagai contoh, fluks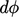 
yang terkait dengan kecepatan melalui segmen permukaan dengan luas (dS) akan menjadi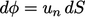 
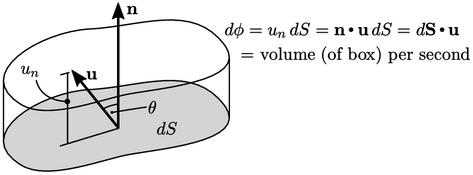
Seperti yang ditujukkan dalam gambar,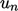 
dapat dihitung dari (n) dengan produk dalam dengan vector normal (n) yang memiliki panjang satuan, dinyatakan sebagai berikut:
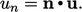 | (2.5) |
Fluks yang terkait dengan (u) adalah
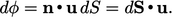 | (2.6) |
Merupakan kebiasaan baik untuk menuliskan (dS) terlebih dahulu karena urutan penting Dungan tensor, misalnya, tegangan (0) yang diperkenalkan pads bagian 2.6, yaitu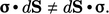 
Inner Produk dari dua vektor
Komponen normal dari kecepatan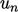 
, seperti yang dijelaskan dalam persamaan (2.5) dengan produk dalam, atau produk “dot” dari (u) dan (n). Ini dihitung untuk vector – vektor (a) dan (b) seperti yang ditunjukkan gambar di bawah ini, dimana |…| menunjukkan magnitude dari vector dan 
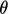adalah sudut internal antara kedua vector tersebut
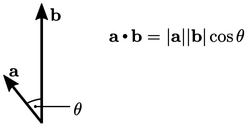
Produk dalam dari dua vector adalah scalar invarian, karena magnitudo dan sudutnya sama tanpa memandang sistem koordinat yang digunakan. Ini dihitung dari komponen vector sebagai berikut :
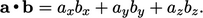
Produk dalam dari dua vektor bersifat komutatif, artinya a.b = b.a. Ini bersifat distributif, artinya dengan vector tambahan c.
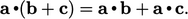
Perkalian skalar dan produk dalam bersifat asosiatif, artinya;
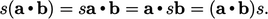
Produk dalam dari sebuah vektor dengan dirinya sendiri adalah kuadrat dari magnitudo vektor, artinya;
 |
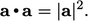(2.7) |