Diskritisasi Gradien

Diskritisasi gradien 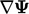$persamaan$ secara eksklusif merupakan penghitungan eksplisit menggunakan nilai saat ini 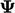$persamaan$ . Bentuk konservatif perhitungan gradien didasarkan pada integral permukaan.

$GAMBAR\santai \khusus {t4ht=$

Dari definisi gradien di Sec. 2.23, diskritisasinya adalah

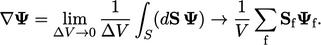1 Z 1 X r = lVim!0 -V-- (dS ) ! V- Sf f: S f \relax \special {t4ht=

(3.18)

Nilai nominal 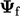$persamaan$ umumnya diinterpolasi dari nilai sel menggunakan skema linier.

Interpolasi linier titik

Meskipun kemiringan secara umum tidak menjadi perhatian dalam diskritisasi adveksi, hal ini perlu mendapat perhatian lebih besar dalam penghitungan gradien. Untuk mesh yang “buruk”, misalnya mengandung sel tetrahedral yang memanjang, skema titik linier sering digunakan untuk mengurangi kesalahan kemiringan.

Interpolasi linier titik menggunakan: nilai 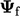$persamaan$ , dihitung menggunakan interpolasi linier, yang sesuai dengan “titik muka” di perpotongan garis yang menghubungkan pusat sel dan muka; dan, nilai 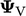$persamaan$ pada setiap titik, diinterpolasi dari sel yang berdekatan menggunakan pembobotan jarak terbalik.

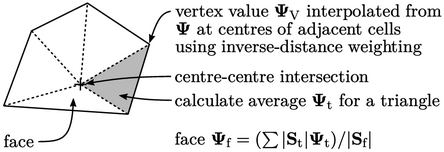
$GAMBAR\santai \khusus {t4ht=$

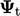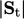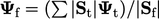Skema ini memecah permukaan poligonal menjadi segitiga dan menghitung nilai rata-rata $persamaan$ pada 2 simpul dan titik permukaan untuk setiap segitiga, luas $persamaan$ . Interpolasi titik menghitung nilai nominal sebagai rata-rata tertimbang luas dari nilai-nilai segitiga, yaitu $persamaan$ .

Gradien kuadrat terkecil

Penghitungan gradien menggunakan metode beda hingga kuadrat terkecil terkadang digunakan dalam kerangka volume hingga. Metode ini menghitung gradien dalam sel yang, bila digunakan untuk mengekstrapolasi nilai sel ke pusat semua sel tetangga, meminimalkan kesalahan antara nilai ekstrapolasi dan nilai sel.

Untuk sel tertentu, tensor 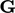$persamaan$ dihitung dengan menjumlahkan permukaan menggunakan pembobotan jarak terbalik 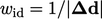$persamaan$ , dimana 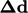$persamaan$ adalah vektor pusat-pusat sel:

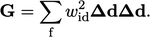X 2 G = w id d d: f \relax \special {t4ht=

(3.19)

Gradien kemudian dievaluasi menggunakan kebalikan dari tensor 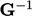$persamaan$ dan nilai di sel tetangga (N) dan sel saat ini (P):

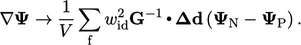1-X 2 1 r ! V w idG d( N P): f \relax \special {t4ht=

(3.20)