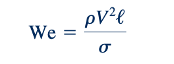Grup Tak Berdimensi yang Umum dalam Mekanika Fluida
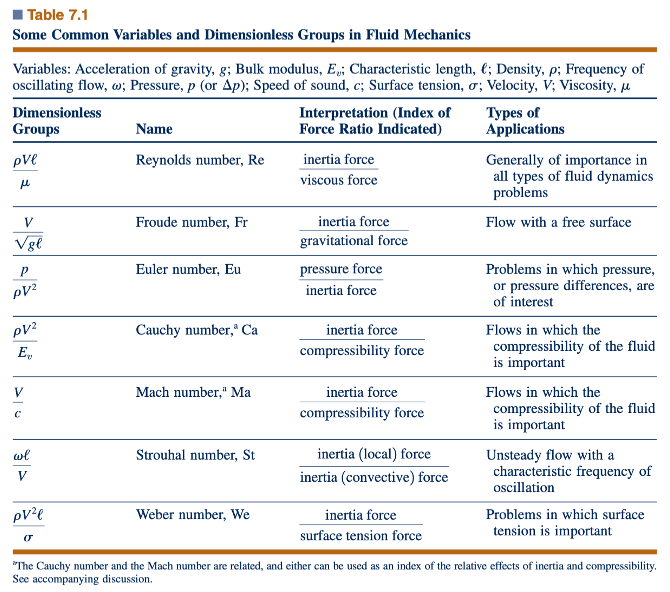
Grup Tak Berdimensi yang Umum dalam Mekanika Fluida. Di bagian atas Tabel 7.1 terdapat daftar variabel yang umum muncul dalam masalah mekanika fluida. Daftar tersebut jelas tidak lengkap namun memberikan gambaran luas tentang beragam variabel yang mungkin ditemui dalam masalah tipikal. Untungnya, tidak semua variabel ini akan dijumpai dalam setiap masalah. Namun, ketika kombinasi dari variabel-variabel ini hadir, adalah praktik standar untuk menggabungkannya menjadi beberapa kelompok dimensi yang umum (pi terms) yang tercantum di Tabel 7.1. Kombinasi-kombinasi ini muncul begitu sering sehingga memiliki nama khusus yang terkait dengan mereka, sebagaimana ditunjukkan dalam tabel.
Juga sering kali mungkin untuk memberikan interpretasi fisik terhadap kelompok-kelompok dimensi yang tidak bersifat dimensi, yang dapat membantu dalam menilai pengaruh mereka dalam suatu aplikasi tertentu. Sebagai contoh, angka Froude adalah indeks dari rasio gaya yang disebabkan oleh percepatan partikel fluida terhadap gaya yang disebabkan oleh gravitasi (berat). Ini dapat ditunjukkan dengan mempertimbangkan partikel fluida yang bergerak sepanjang garis arus (Gambar 7.3). Besarnya komponen gaya inersia FI sepanjang garis arus dapat dinyatakan sebagai F1= as, m, di mana a adalah besarnya percepatan sepanjang garis arus untuk sebuah partikel dengan massa m. Dari studi kita tentang gerak partikel sepanjang lintasan melengkung (lihat Bagian 3.1) kita tahu bahwa.
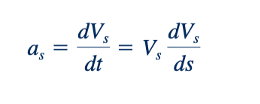
Jika kita menuliskan kecepatan, Vs, dan panjang, s, dalam bentuk tanpa dimensi,
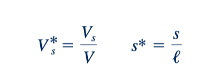
di mana V dan ℓ mewakili kecepatan karakteristik dan panjang, secara berturut-turut,
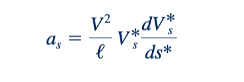
Dan
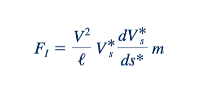

Magnitudo berat partikel, FG, adalah FG gram, sehingga rasio inersia terhadap gaya gravitasi adalah
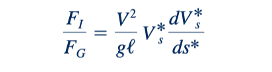
Dengan demikian, rasio gaya F1/FG berkaitan proporsional dengan V2g/ℓ, dan akar kuadrat dari rasio ini, 𝑉/√𝑔ℓ, disebut angka Froude.Kita melihat bahwa interpretasi fisik dari angka Froude adalah bahwa itu adalah sebuah ukuran, atau indeks, dari pentingnya relatif gaya inersia yang bekerja pada partikel fluida terhadap berat partikel tersebut. Perlu dicatat bahwa angka Froude sebenarnya tidak sama dengan rasio gaya ini, namun merupakan jenis pengukuran rata-rata dari pengaruh kedua gaya tersebut. Dalam masalah di mana gravitasi atau berat tidak penting, angka Froude tidak akan muncul sebagai pi term yang penting. Interpretasi serupa dalam hal indeks rasio gaya dapat diberikan kepada kelompok tanpa dimensi lainnya, sebagaimana ditunjukkan dalam Tabel 7.1, dan diskusi lebih lanjut tentang dasar untuk jenis interpretasi ini diberikan dalam bagian terakhir dalam bab ini. Beberapa detail tambahan tentang kelompok tanpa dimensi penting ini diberikan di bawah ini, dan jenis aplikasi atau masalah di mana mereka muncul secara singkat dicatat dalam kolom terakhir Tabel 7.1.
Nomor Reynolds: Nomor Reynolds tanpa ragu adalah parameter tanpa dimensi yang paling terkenal dalam mekanika fluida. Ini dinamai untuk menghormati Osborne Reynolds (1842–1912), seorang insinyur Britania yang pertama kali menunjukkan bahwa kombinasi variabel ini dapat digunakan sebagai kriteria untuk membedakan aliran laminar dan turbulen. Dalam sebagian besar masalah aliran fluida, akan ada panjang karakteristik, ℓ, dan kecepatan, V, serta sifat-sifat fluida seperti densitas, ρ, dan viskositas, μ, yang merupakan variabel-variabel yang relevan dalam masalah tersebut. Dengan demikian, dengan variabel-variabel ini, nomor Reynolds
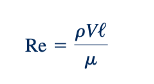
Timbul secara alami dari analisis dimensional. Nomor Reynolds adalah sebuah ukuran dari rasio gaya inersia pada suatu elemen fluida terhadap gaya kental pada elemen tersebut. Ketika kedua jenis gaya ini penting dalam suatu masalah tertentu, nomor Reynolds akan memainkan peran penting. Namun, jika nomor Reynolds sangat kecil (Re ≈ 1), ini menunjukkan bahwa gaya kental mendominasi masalah tersebut, dan mungkin memungkinkan untuk mengabaikan efek inersia; yaitu, densitas fluida tidak akan menjadi variabel yang penting. Aliran pada nomor Reynolds yang sangat kecil umumnya disebut sebagai "aliran merayap", seperti yang dibahas dalam Bagian 6.10. Sebaliknya, untuk aliran pada nomor Reynolds yang besar, efek kental kecil dibandingkan dengan efek inersia dan untuk kasus-kasus ini mungkin memungkinkan untuk mengabaikan efek viskositas dan mempertimbangkan masalah sebagai salah satu yang melibatkan fluida "nonviskous". Jenis masalah ini dibahas secara detail dalam Bagian 6.4 hingga 6.7. Sebuah contoh pentingnya nomor Reynolds dalam menentukan fisika aliran ditunjukkan dalam gambar di sisi untuk aliran di sekitar silinder berbentuk lingkaran pada dua nilai Re yang berbeda. Aliran ini dibahas lebih lanjut dalam Bab 9.
Nomor Froude. Nomor Froude
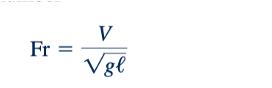
membedakan dari kelompok tanpa dimensi lainnya dalam Tabel 7.1 karena mengandung percepatan gravitasi, g. Percepatan gravitasi menjadi variabel penting dalam masalah dinamika fluida di mana berat fluida merupakan gaya penting. Seperti yang dibahas, angka Froude adalah sebuah ukuran dari rasio gaya inersia pada suatu elemen fluida terhadap berat elemen tersebut. Umumnya, hal ini akan penting dalam masalah yang melibatkan aliran dengan permukaan bebas karena gravitasi pada dasarnya memengaruhi jenis aliran ini. Masalah yang umumnya terjadi akan mencakup studi aliran air di sekitar kapal (dengan aksi gelombang yang dihasilkan) atau aliran melalui sungai atau saluran terbuka. Angka Froude dinamai untuk menghormati William Froude (1810–1879), seorang insinyur sipil, matematikawan, dan arsitek kelautan Britania yang memimpin penggunaan tangki tarik untuk studi desain kapal. Perlu dicatat bahwa angka Froude juga sering didefinisikan sebagai kuadrat dari angka Froude yang tercantum dalam Tabel 7.1.
Nomor Euler. Nomor Euler

dapat diinterpretasikan sebagai ukuran dari rasio gaya tekanan terhadap gaya inersia, di mana p adalah tekanan karakteristik dalam medan aliran. Seringkali, angka Euler ditulis dalam hal perbedaan tekanan, Δp, sehingga Eu = Δp / ρV². Juga, kombinasi ini yang diekspresikan sebagai Δp /1/2 ρV² disebut sebagai koefisien tekanan. Beberapa bentuk angka Euler biasanya digunakan dalam masalah di mana tekanan atau perbedaan tekanan antara dua titik merupakan variabel penting. Angka Euler dinamai untuk menghormati Leonhard Euler (1707–1783), seorang matematikawan Swiss terkenal yang memimpin karya tentang hubungan antara tekanan dan aliran. Untuk masalah di mana kavitasi menjadi perhatian, kelompok tanpa dimensi (pr - pv) / 1/2 ρV² sering digunakan, di mana pv adalah tekanan uap dan pr adalah tekanan referensi. Meskipun kelompok tanpa dimensi ini memiliki bentuk yang sama dengan angka Euler, umumnya disebut sebagai angka kavitasi.
Nomor Cauchy dan Nomor Mach. Nomor Cauchy
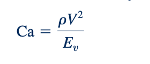
dan bilangan Mach
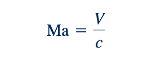
Merupakan kelompok tak berdimensi yang tidak penting dalam permasalahan yang mana kompresibilitas fluida merupakan faktor yang signifikan. karena cepat rambat bunyi, c dalam suatu fluida sama dengan 𝑐=√(𝐸𝑣/𝜌) , (lihat bagian 1.7.3 )
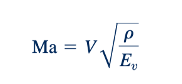
dan kuadrat bilangan Mach
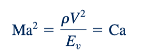
sama dengan nomor Cauchy. Dengan demikian, salah satu nomor ini (tapi tidak keduanya) dapat digunakan dalam masalah di mana kompresibilitas fluida penting. Kedua nomor dapat diinterpretasikan sebagai representasi indeks dari rasio gaya inersia terhadap gaya kompresibilitas. Ketika nomor Mach relatif kecil (misalnya, kurang dari 0.32), gaya inersia yang diinduksi oleh gerakan fluida tidak cukup besar untuk menyebabkan perubahan signifikan dalam densitas fluida, dan dalam kasus ini, kompresibilitas fluida dapat diabaikan. Nomor Mach adalah parameter yang lebih umum digunakan dalam masalah aliran yang dapat dikompresi, terutama dalam bidang dinamika gas dan aerodinamika. Nomor Cauchy dinamai untuk menghormati Augustin Louis de Cauchy (1789–1857), seorang insinyur, matematikawan, dan ahli hidrodinamika Prancis. Nomor Mach dinamai untuk menghormati Ernst Mach (1838–1916), seorang fisikawan dan filsuf Austria.
Nomor Strouhal. Nomor Strouhal

adalah sebuah parameter tanpa dimensi yang kemungkinan penting dalam masalah aliran yang tidak stabil dan berayun di mana frekuensi ayunan adalah v. Ini merupakan sebuah ukuran dari rasio gaya inersia akibat ketidakstabilan aliran (akselerasi lokal) terhadap gaya inersia akibat perubahan kecepatan dari titik ke titik dalam medan aliran (akselerasi konvektif). Jenis aliran tidak stabil seperti ini dapat berkembang ketika fluida mengalir melewati benda padat (seperti kawat atau kabel) yang ditempatkan dalam aliran bergerak. Sebagai contoh, dalam rentang nomor Reynolds tertentu, aliran periodik akan berkembang di hilir dari sebuah silinder yang ditempatkan dalam fluida bergerak karena pola reguler pusaran yang terlepas dari benda tersebut. Sistem pusaran ini, yang disebut jejak pusaran Kármán [dinamai menurut Theodor von Kármán (1881–1963), seorang ahli fluida terkenal], dapat dilihat pada foto di awal bab ini dan pada Gambar 9.21.menciptakan aliran yang berayun pada frekuensi diskrit, v, sehingga nomor Strouhal dapat berkorelasi erat dengan nomor Reynolds. Ketika frekuensi berada dalam rentang yang dapat didengar, suara dapat terdengar dan benda-benda tersebut tampak "bernyanyi." Faktanya, nomor Strouhal dinamai untuk menghormati Vincenz Strouhal (1850–1922), yang menggunakan parameter ini dalam studinya tentang "kawat yang bernyanyi." Bukti paling dramatis dari fenomena ini terjadi pada tahun 1940 dengan runtuhnya Jembatan Tacoma Narrows. Frekuensi lepasan pusaran bersamaan dengan frekuensi alami jembatan, sehingga menimbulkan kondisi resonansi yang akhirnya menyebabkan runtuhnya jembatan.
Tentu saja, ada jenis aliran yang berayun lainnya. Sebagai contoh, aliran darah di arteri bersifat periodik dan dapat dianalisis dengan memecah gerakan periodik menjadi serangkaian komponen harmonik (analisis deret Fourier), dengan setiap komponen memiliki frekuensi yang merupakan kelipatan dari frekuensi fundamental, v (laju detak jantung). Alih-alih menggunakan nomor Strouhal dalam jenis masalah ini, kelompok tanpa dimensi yang terbentuk dari produk St dan Re digunakan; yaitu
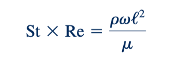
Akar kuadrat dari kelompok tanpa dimensi ini sering disebut sebagai parameter frekuensi.
Nomor Weber. Nomor Weber