2.3 MATRIKS DAN OPERASI MATRIKS
Matriks dan operasi matriks. Matriks A berordo M × N adalah susunan berbentuk persegi panjang dari kuantitas (bilangan atau ekspresi) yang disusun dalam M baris dan N kolom [9–11]. Elemen dari A yang terletak pada baris ke-i dan kolom ke-j ditandai dengan aij. Sebagai contoh, elemen a32 dari matriks berordo 4 × 3 yang ditunjukkan pada Gambar 2.10 adalah 12.
Berdasarkan definisi ini, dapat disimpulkan bahwa vektor kolom v berdimensi N adalah suatu matriks berordo N × 1, dan skalar s adalah suatu matriks berordo 1 × 1.
Transpose dari suatu matriks A berordo M × N adalah matriks lain yang ditandai dengan AT berordo N × M, di mana baris-baris A menjadi kolom-kolom AT, dan kolom-kolom A menjadi baris-baris AT. Secara matematis, ini dapat dituliskan sebagai,

Dua matriks yang memiliki ordo yang sama dianggap sama jika elemen-elemen yang sesuai di antara keduanya adalah sama. Dua matriks yang memiliki ordo yang sama dapat dijumlahkan atau dikurangkan secara elemen demi elemen. Sebagai contoh, jika A dan B diberikan oleh,

maka A + B dan A – B ditemukan sebagai berikut,

Jika suatu matriks dikalikan dengan skalar s, maka semua elemennya akan dikalikan dengan s. Secara matematis, hal ini dituliskan sebagai,

Untuk mengalikan dua matriks A dan B, jumlah kolom pada A harus sama dengan jumlah baris pada B. Oleh karena itu, jika A memiliki ukuran M × X untuk hasil kali P = AB,

untuk menjadi mungkin, B harus berukuran X × N. Ukuran dari P akan menjadi M × N dengan elemen-elemen pij yang diperoleh sebagai,
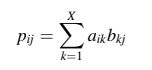
Jika A adalah matriks 3 × 2 dan B adalah matriks 2 × 4 yang diberikan oleh,

maka P = AB akan menjadi matriks 3 × 4 yang dihitung sebagai,

