4.1.2 Step II: Domain Discretization

Domain discretization. Diskritisasi geometris dari domain fisik menghasilkan suatu jala di mana persamaan konservasi akhirnya dipecahkan. Ini memerlukan subdivisi domain menjadi sel atau elemen diskrit non-tumpang tindih yang mengisi seluruh domain komputasi untuk menghasilkan sistem jala atau mesh. Ini dicapai dengan berbagai teknik yang menghasilkan berbagai jenis jala. Jenis-jenis jala ini diklasifikasikan berdasarkan beberapa karakteristik: struktur, ortogonalitas, blok, bentuk sel, susunan variabel, dll. Dalam semua kasus, jala terdiri dari elemen diskrit yang didefinisikan oleh satu set verteks dan dibatasi oleh wajah-wajah.

Agar jala menjadi platform yang berguna untuk diskritisasi persamaan, informasi yang terkait dengan topologi elemen jala, ditambah beberapa informasi geometris turunan, diperlukan. Ini mencakup hubungan elemen ke elemen, hubungan wajah ke elemen, informasi geometris permukaan, pusat massa dan volume elemen, pusat massa wajah, area, dan arah normal, dll. Informasi ini biasanya disimpulkan dari data jala dasar.

Untuk beberapa topologi jala, detail tentang jala dapat dengan mudah diambil dari indeks elemen seperti pada grid terstruktur, sedangkan untuk yang lainnya harus dibangun dan disimpan dalam daftar untuk diambil nanti, seperti pada kasus grid tidak terstruktur.

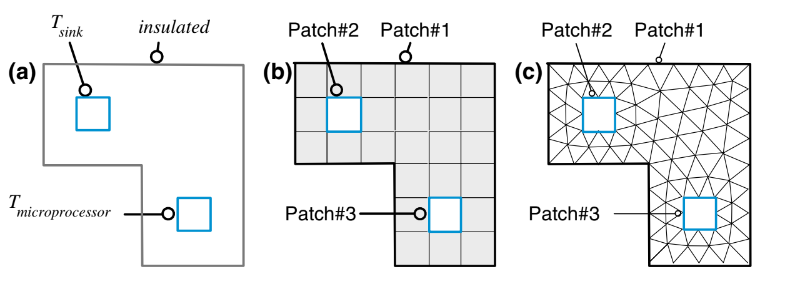
pertimbangkan domain sederhana yang ditunjukkan pada Gambar 4.3a. Domain ini terdiri dari suatu volume (luas untuk kasus dua dimensi) dan batas yang memperhitungkan pemanasan atau pendinginan dari mikroprosesor, heatsink, dan dasar penyebar panas. Domain tersebut ditunjukkan terdiskritisasi dengan jala sederhana pada Gambar 4.3b. Batas jala dibagi menjadi tiga patch dari wajah batas yang diberi nomor, yaitu Patch#1, Patch#2, dan Patch#3. Patch ini digunakan untuk menentukan kondisi batas fisik untuk masalah yang sedang dihadapi. Jala tersebut terdiri dari 25 elemen non-tumpang tindih yang geometrinya didefinisikan oleh 40 titik (vertiks sel). Elemen-elemen ini juga dibatasi oleh 66 wajah (garis dalam kasus dua dimensi), 34 di antaranya adalah wajah interior.

Persamaan aljabar yang muncul dari diskritisasi persamaan pemimpin, sebagaimana akan dijelaskan dalam langkah III, dijelaskan untuk setiap elemen dalam domain komputasi dengan solusi diungkapkan sebagai lapangan elemen dengan nilai yang didefinisikan di pusat massa setiap elemen. Dalam contoh ini, elemen-elemen memiliki bentuk persegi, meskipun bentuk lain dapat digunakan (misalnya, elemen segitiga, seperti yang ditunjukkan pada Gambar 4.3c).

Jala dapat dijelaskan dari perspektif yang berbeda. Pada tingkat paling dasar, ini adalah daftar verteks atau titik yang mewakili lokasi dalam ruang satu dimensi, dua dimensi, atau tiga dimensi. Jala juga mewakili domain yang terdiskritisasi yang dibagi menjadi elemen-elemen non-tumpang tindih, yang dapat berbentuk polihedral konveks sembarang. Elemen sepenuhnya dibatasi oleh wajah yang umumnya dibagi oleh elemen tetangga, kecuali di batas. Elemen dapat didefinisikan baik dalam hal titik yang membatasi mereka maupun dalam hal wajah yang membatasi mereka. Wajah jala, yang disimpan dalam daftar, memiliki dua tipe: (i) wajah interior yang dibagi (atau menghubungkan) dua elemen, dan (ii) wajah batas yang bertepatan dengan batas domain; wajah batas ini hanya memiliki satu elemen yang berdekatan. Sementara wajah interior diperoleh dari informasi yang terkait dengan topologi elemen, penting untuk menyediakan wajah batas karena mereka menentukan batas fisik domain. Dalam dua dimensi, wajah dijelaskan dalam hal titik-titik penentu mereka. Dalam tiga dimensi, titik-titik penentu menggambarkan tepi yang membatasi wajah. Arah normal ke wajah interior biasanya didefinisikan berdasarkan topologi elemen tetangga. Di sisi lain, arah dari

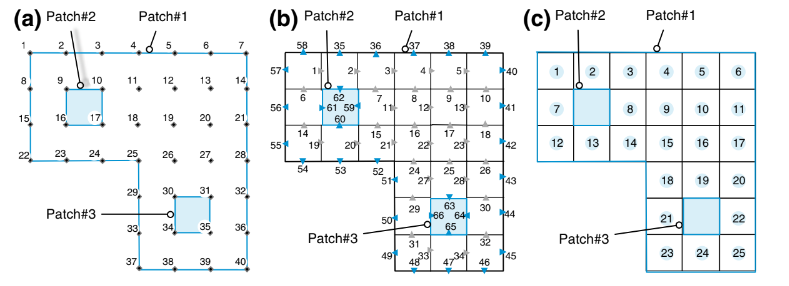
normal ke wajah batas selalu mengarah keluar dari domain. Gambar 4.4 menunjukkan beberapa komponen (vertiks, wajah, dan elemen yang ditunjukkan pada Gambar 4.4a–c secara berurutan) dari sebuah jala. Selain itu, wajah batas diorganisir menjadi daftar wajah berdasarkan patch batas ke mana mereka termasuk.