4.1.4 Step III: Equation Discretization
Equation discretization. Dalam langkah III, persamaan diferensial parsial yang mengatur diubah menjadi serangkaian persamaan aljabar, satu untuk setiap elemen dalam domain komputasi. Persamaan aljabar ini kemudian dirangkai menjadi matriks global dan vektor yang dapat dinyatakan dalam bentuk menerjemahkan Indonesia.
Di mana variabel yang tidak diketahui T didefinisikan di setiap elemen interior dan di batas domain komputasi. Nilai-nilai batas untuk T umumnya diperoleh dari kondisi batas yang ditentukan. Untuk ini, sebuah lapangan elemen harus didefinisikan untuk T, dan umumnya untuk setiap persamaan yang mengatur.
Seperti yang ditunjukkan secara skematis dalam Figur 4.10, lapangan elemen terdiri dari sebuah array nilai yang didefinisikan di centroid setiap elemen, ditunjuk oleh lapangan elemen interior, yang direpresentasikan oleh satu array dengan ukuran sama dengan jumlah total elemen interior dan batas.
Langkah diskritisasi persamaan dilakukan di atas setiap elemen domain komputasi untuk menghasilkan hubungan aljabar yang menghubungkan nilai suatu variabel
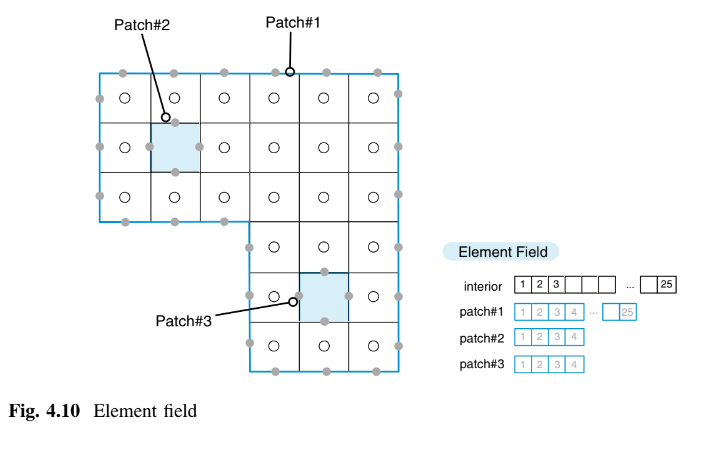
dalam sebuah elemen terhadap nilai variabel di elemen-elemen tetangga. Persamaan aljabar ini diperoleh dengan melakukan diskritisasi persamaan diferensial, yang untuk contoh yang dipertimbangkan adalah persamaan energi yang ditulis dalam istilah suhu T (yaitu, T adalah variabel yang tidak diketahui). Seperti yang ditunjukkan di bawah ini, dalam metode volume hingga, diskritisasi persamaan dilakukan dengan pertama-tama mengintegrasikan persamaan diferensial di atas suatu volume kontrol atau sel untuk memperoleh bentuk semi-diskritisasi dari persamaan tersebut, kemudian mendekati variasi variabel tergantung antara elemen grid melalui profil yang diberlakukan untuk memperoleh bentuk diskritisasi final. Fakta bahwa hanya beberapa elemen grid yang berpartisipasi dalam suatu persamaan diskritisasi yang diberikan adalah konsekuensi dari sifat bertahap dari profil yang dipilih. Nilai T di suatu titik grid mempengaruhi distribusi T hanya di lingkungan sekitarnya. Seiring dengan peningkatan jumlah elemen grid, solusi dari persamaan diskritisasi diharapkan mendekati solusi eksak dari persamaan diferensial yang sesuai. Ini mengikuti dari pertimbangan bahwa, ketika elemen grid mendekat satu sama lain, perubahan dalam T antara elemen grid tetangga menjadi kecil, dan maka detail aktual dari asumsi profil menjadi tidak penting. Untuk sebuah persamaan diferensial yang diberikan, persamaan diskritisasi yang mungkin tidak unik, meskipun semua jenis teknik diskritisasi dalam batas jumlah elemen grid yang sangat besar diharapkan memberikan solusi yang sama. Berbagai jenis muncul dari perbedaan dalam asumsi profil dan metode derivasi. Sebagai contoh dari langkah diskritisasi persamaan menggunakan metode volume hingga, bentuk diskritisasi dari persamaan energi di atas volume kontrol C yang ditunjukkan dalam Figur (4.11) dicari. Proses dimulai dengan mengintegrasikan Persamaan (4.1) di atas elemen C yang memungkinkan pemulihan bentuk keseimbangan integralnya, yang dijelaskan dalam Bab 3, sebagai.
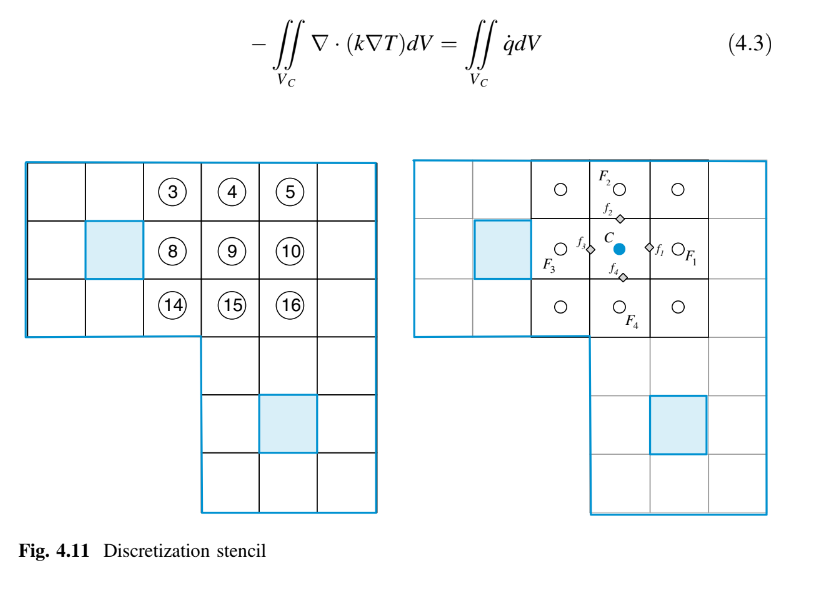
Kemudian, dengan menggunakan teorema divergensi, integral volume diubah menjadi integral permukaan menghasilkan.

Persamaan ini pada dasarnya adalah keseimbangan panas di atas elemen C. Ini merupakan bentuk integral dari persamaan diferensial parsial asli dan tidak melibatkan aproksimasi apa pun. Dengan menggantikan integral permukaan dengan penjumlahan atas wajah-wajah volume kontrol, Persamaan (4.4) berubah menjadi:
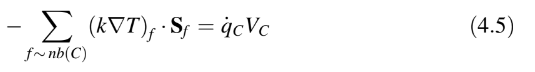
di mana f mewakili titik integrasi di centroid wajah pembatas. Transformasi ini merupakan aproksimasi pertama yang diperkenalkan. Oleh karena itu, integral dalam Persamaan (4.4) diaproksimasi secara numerik oleh fluks di centroid wajah. Ini merupakan aproksimasi orde kedua seperti yang akan ditunjukkan dalam bab selanjutnya. Dengan memperluas penjumlahan, Persamaan (4.5) dapat ditulis sebagai:
Mempertimbangkan wajah f1 yang ditunjukkan dalam Figur (4.12), vektor permukaan dan gradien suhu dalam Persamaan (4.6) diberikan oleh


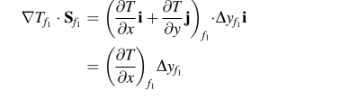
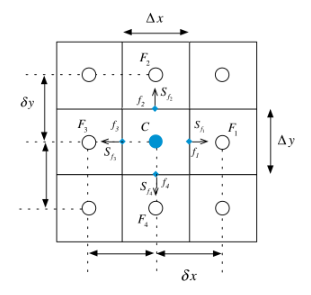
Untuk melanjutkan, diperlukan profil yang mendekati variasi T antara C dan F1Dengan mengasumsikan variasi linear dari T, komponen-x dari gradien di wajah dapat ditulis sebagai.

Dengan demikian, Persamaan (4.8) dapat diaproksimasi sebagai.
atau lebih umum sebagai
dimana

Mengulangi untuk setiap wajah yang tersisa, koefisien berikut diperoleh:
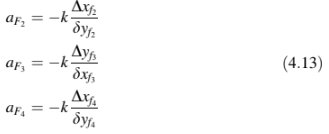
yang ketika disubstitusikan ke dalam Persamaan (4.6) menghasilkan.
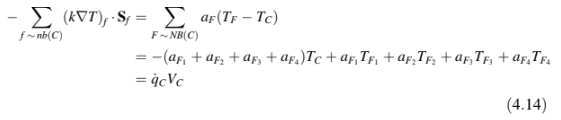
atau lebih padat
dimana
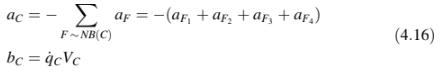
Persamaan serupa dengan Persamaan (4.15) dapat diturunkan untuk semua sel dalam domain, menghasilkan serangkaian persamaan aljabar, yang dapat dipecahkan menggunakan berbagai metode langsung atau iteratif. Berfokus pada elemen C dalam Figur (4.13), Persamaan (4.15) menyiratkan hubungan.
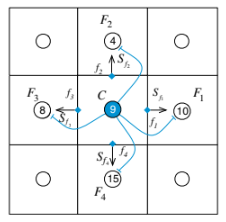

Antara TC dan suhu pada keempat tetangganya, yaitu dan
, yang dalam perakitan global akan menjadi
. Persamaan serupa juga diturunkan untuk elemen batas dan kumpulan mereka menghasilkan serangkaian persamaan yang diilustrasikan dalam Figur (4.14), yang dapat direpresentasikan dalam bentuk matriks seperti yang diberikan dalam Persamaan (4.2), di mana A adalah matriks koefisien, [T] adalah vektor solusi, dan b adalah vektor yang terdiri dari istilah yang tidak dapat disertakan dalam A. Metodologi untuk menyelesaikan Persamaan (4.2) disajikan dalam bagian berikutnya. Akhirnya, perlu dinyatakan bahwa sifat-sifat metode volume hingga sehubungan dengan akurasi, kekokohan, dan karakteristik lainnya akan ditinjau dalam bab-bab berikutnya. Ini termasuk pemeriksaan secara lebih detail diskritisasi volume hingga dari istilah difusi, yang telah disajikan di atas untuk grid kartesian berbentuk persegi panjang.
