4.1. Boundary Mesh

Boundary mesh. Pada Bab 3.2 menjelaskan jaringan komputasi yang digunakan oleh metode finite volume. Ini mengidentifikasi batas domain oleh permukaan yang hanya terhubung ke satu sel. Permukaan batas dikelompokkan menjadi patch, masing-masing dengan nama unik, sesuai dengan daerah berbeda dari batas. Kondisi batas kemudian diterapkan pada setiap patch untuk memberikan solusi representatif untuk kasus yang diminati.

Pada contoh aliran dalam pipa, akan logis untuk membagi batas menjadi 3 patch untuk menentukan aliran masuk, aliran keluar, dan dinding padat; dan, inlet, outlet, dan wall akan menjadi nama-nama yang logis untuk patch-patch ini.

Patch Geometry Data

Geometri dari sebuah patch dijelaskan menggunakan data permukaan yang dijelaskan dalam Bab 3.3, termasuk:

vektor area permukaan, 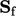, dengan sejumlah area dan arah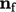
vektor normal satuan permukaan ;
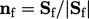pusat permukaan .

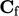Sel sel yang terhubung ke setiap permukaan patch ditandai dengan subskrip “P”, misalnya pusat sel ditandai $\text{[math]}$

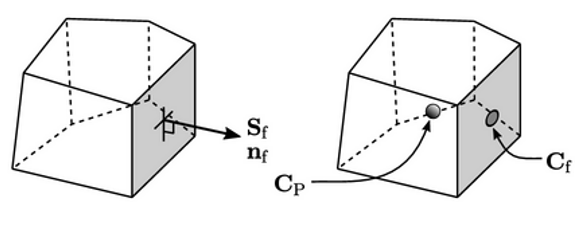
Patch Deltas

Pada Bab 3.8 menjelaskan persamaan “delta“ 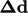untuk setiap wajah sebagai vektor yang menghubungkan pusat sel pemilik dan sel tetangganya. 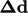Persamaan ini didefinisikan dengan cara yang berbeda untuk permukaan patch karena tidak memiliki sel tetangga.

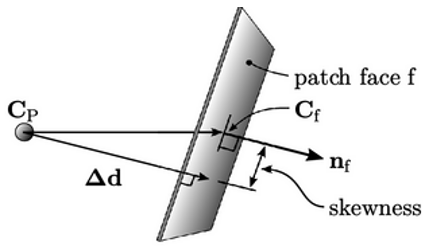
Delta didefinisikan sebagai komponen dari dalam arah normal permukaan. Persamaan gradien permukaan 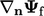bersifat ortogonal terhadap permukaan, yang menghilangkan error yang terkait dengan non-ortogonalitas, namun dengan memperkenalkan error skewness. Mengambil produk dalam dengan 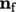memberikan jumlah yang kemudian dikalikan dengan 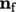untuk menetapkan arahnya, yaitu:

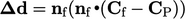d = nf(nf (Cf CP)) \relax \special {t4ht=

(4.1)

Koefisien delta adalah , seperti yang didefinisikan dalam Bab 3.8. Koefisien delta , yang mewakili “inverse distance” atau “jarak terbalik”, merupakan parameter kritis dalam diskritisasi kondisi batas.