4.8. Numerical Framework

Numerical framework. Nilai tetap dan kondisi gradien tetap dijelaskan dalam Sec. 4.2 dapat digabungkan untuk membentuk kerangka numerik umum untuk kondisi batas.

Kontribusi kondisi batas terhadap persamaan matriks 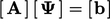$persamaan$ , melalui diskritisasi suku adveksi dan Laplacian, dapat digeneralisasikan sebagai:

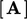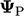kontribusi “ internal $persamaan$ ” ke , dari istilah termasuk nilai sel $persamaan$ ;
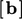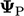kontribusi “ batas $persamaan$ ” ke , dari ketentuan tanpa $persamaan$ .

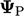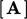Contoh di atas menunjukkan Persamaan. (4.2) untuk nilai nominal, yang diperlukan pada batas diskritisasi adveksi, dalam kasus kondisi batas gradien tetap . “Faktor” internal pada $persamaan$ adalah 1, yang dikalikan dengan $persamaan$ kontribusi terhadap koefisien diagonal masing-masing dalam $persamaan$ , seperti pada contoh di Bagian. 3.24.

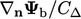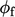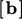Faktor batasnya adalah $persamaan$ , yang juga dikalikan dengan $persamaan$ kontribusinya $persamaan$ .

Untuk kondisi nilai tetap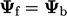 $persamaan$ dengan adveksi , faktor batasnya adalah 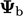$persamaan$ dan faktor internalnya adalah 0.

Diskritisasi Laplacian memerlukan gradien normal permukaan pada permukaannya. Kondisi gradien tetap menghasilkan faktor batas ekuivalen sebesar 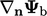$persam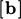aan$ dan $persamaan$ faktor internal sebesar 0.

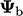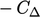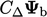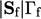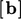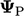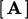Dengan nilai tetap $persamaan$ , persamaan gradien wajah normal. (4.3) memberikan faktor internal $persamaan$ dan faktor batas dari $persamaan$ . Keduanya dikalikan dengan $persamaan$ kontribusinya $persamaan$ dan koefisien diagonal $persamaan$ dalam $persamaan$ , seperti yang ditunjukkan dalam diskritisasi Laplacian di Bagian. 3.24.

Tabel di bawah ini merangkum: faktor internal dan batasan “nilai”, yang berkontribusi terhadap koefisien matriks masing-masing dengan diskritisasi adveksi; dan faktor “gradien” yang setara terkait dengan diskritisasi Laplacian. Hal ini memberikan kerangka kerja yang dapat diperluas ke kondisi yang lebih kompleks.