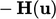5.10 Kopling tekanan-kecepatan
Kopling tekanan-kecepatan. Bagian sebelumnya menggabungkan persamaan untuk 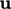 dan
dan 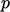 , yang mengatur momentum dan konservasi massa, dalam sebuah solusi berurutan. Algoritma yang digunakan untuk menggabungkan persamaan-persamaan ini, dengan cara yang konvergen, menggunakan notasi berikut untuk menjelaskan istilah-istilah dalam persamaan momentum, misalnya Persamaan (2.67), kecuali
, yang mengatur momentum dan konservasi massa, dalam sebuah solusi berurutan. Algoritma yang digunakan untuk menggabungkan persamaan-persamaan ini, dengan cara yang konvergen, menggunakan notasi berikut untuk menjelaskan istilah-istilah dalam persamaan momentum, misalnya Persamaan (2.67), kecuali 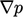 .
.
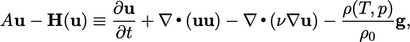 | (5.16) |
Persamaan tersebut memberikan pembaruan untuk u, berdasarkan nilai saat ini dari u dan p yang digantikan di sisi sebelah kanan. Dengan kata lain, 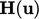 dan
dan 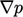 dihitung secara eksplisit.
dihitung secara eksplisit.
Dalam algoritma yang dijelaskan pada bagian-bagian berikutnya, A dipilih sebagai koefisien diagonal yang diekstraksi a_(i,i) i=1,2,. . . ,N dari matriks A yang sesuai dengan istilah momentum dalam Persamaan (5.16).
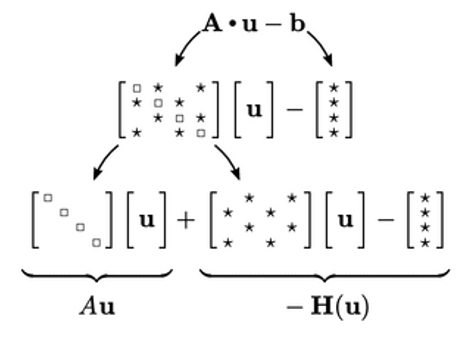
Pemisahan antara 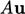 dan
dan 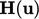 ditunjukkan di atas. Sebagai matriks dengan komponen diagonal saja, A memiliki satu nilai per sel sehingga dapat diwakili sebagai medan skalar. Menetapkan A sebagai koefisien diagonal adalah pilihan yang alami untuk perlakuan implisit terhadap u dalam algoritma kopling.
ditunjukkan di atas. Sebagai matriks dengan komponen diagonal saja, A memiliki satu nilai per sel sehingga dapat diwakili sebagai medan skalar. Menetapkan A sebagai koefisien diagonal adalah pilihan yang alami untuk perlakuan implisit terhadap u dalam algoritma kopling.
Korektor fluks
Persamaan korektor fluks mengikuti dari Persamaan (5.17) dengan interpolasi u ke wajah sel dan mengevaluasi 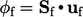 sesuai dengan
sesuai dengan
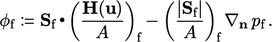 | (5.18) |
Persamaan tekanan
kemudian dibuat dengan menggantikan fluks  dari Persamaan (5.18) ke dalam Persamaan konservasi massa (2.46) dalam bentuk diskrit
dari Persamaan (5.18) ke dalam Persamaan konservasi massa (2.46) dalam bentuk diskrit 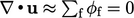 . Ekspresi yang dihasilkan setara dengan sebuah persamaan tekanan yang terdiskritisasi, dengan koefisien yang berisi
. Ekspresi yang dihasilkan setara dengan sebuah persamaan tekanan yang terdiskritisasi, dengan koefisien yang berisi 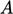 dan
dan 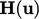 .
.
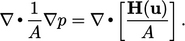 | (5.19) |

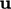 ;
;