5.13 Konvergensi keadaan mantap (steady-state)

Konvergensi keadaan mantap (steady state). Ketidakhadiran turunan waktu dari persamaan yang ditulis dalam bentuk keadaan mantap mengurangi dominasi diagonal, dan dengan demikian, konvergensi dari persamaan matriks yang dihasilkan, seperti yang dibahas di Bagian 5.5. Pengurangan relaksasi kemudian diterapkan pada persamaan T, u, dan p untuk mempromosikan konvergensi dalam algoritma di Bagian 5.12.

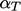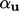Bidang T dan u menggunakan relaksasi persamaan dengan faktor dan , secara berturut-turut. Nilai 0.7 umumnya diterapkan, berkurang menjadi 0.5 untuk kasus yang kurang konvergen (dan terkadang menjadi 0.3 dalam kasus aliran yang dapat dipadatkan, di luar cakupan buku ini).

Pengurangan relaksasi dari p lebih halus. Korektor fluks mengharuskan agar p tidak direlaksasi berlebihan untuk memastikan 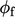mematuhi konservasi massa dengan lebih baik. Untuk korektor momentum, relaksasi bidang kemudian diterapkan pada p dengan faktor 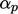. Untuk menemukan faktor optimal 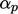untuk korektor momentum, kita memeriksa

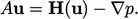Au = H(u) rp: \relax \special {t4ht=

(5.22)

Persamaan momentum eksplisit ini berisi koefisien diagonal A dan kontribusi di luar diagonal 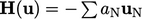dari koefisien sel tetangga 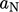dan kecepatan terkait ..

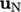Konvergensi terganggu oleh sifat eksplisit dari 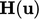. Ini dapat menjadi lebih implisit dengan “menambahkan dan mengurangkan” 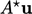, di mana koefisien diterapkan pada u di sel “pemilik

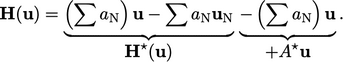H(u) = X a u X a u X a u : |-------------N---------------{z----------------N----------N--} |--------------{z--N------------} H?(u) +A?u \relax \special {t4ht=

(5.23)

Gabungan Persamaan (5.22) dan Persamaan (5.23) memberikan

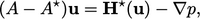? ? (A A )u = H (u) rp; \relax \special {t4ht=

(5.24)

yang berupaya membuat Persamaan (5.22) lebih implisit dalam u. Persamaan tekanan yang berasal dari Persamaan (5.24) adalah;

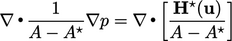$? r ---1---rp = r H--(u)- A A? A A? \relax \special {t4ht=$

(5.25)

Ini sesuai dengan pengurangan relaksasi Persamaan (5.19) sebesar 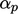, di mana 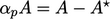. Matriks momentum 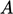dengan koefisien 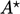kurang lebih setara secara diagonal karena tidak ada turunan waktu. Karena 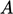mewakili koefisien diagonal yang direlaksasi dengan 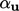, 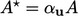. Menghubungkan ekspresi untuk 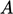dan 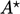memberikan faktor relaksasi optimal untuk p untuk konvergensi sebagai

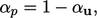$p = 1 u; \relax \special {t4ht=$

(5.26)

pilihan paling populer adalah 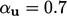dan .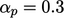

Kontrol Residual

Algoritma dalam Bagian 5.12 menggunakan jumlah langkah solusi yang tetap 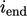. Secara praktis, 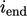. harus dipilih cukup besar untuk mencapai tingkat konvergensi yang dapat diterima. Begitu konvergensi tercapai, simulasi harus dihentikan untuk menghindari biaya komputasi yang tidak perlu.

Kriteria berhenti umum menerapkan tingkat residual untuk setiap persamaan, di bawah mana persamaan dianggap telah konvergen. Ketika semua persamaan memenuhi kontrol residual masing-masing, maka simulasi dihentikan.

Konvergensi juga dapat ditentukan dengan memantau metrik yang sesuai, termasuk pengukuran objektif dari simulasi, misalnya koefisien gaya. Ketika metrik tidak lagi berubah secara signifikan selama langkah-langkah berikutnya, maka simulasi dihentikan.