5.14 Metode penurunan

Metode penurunan. Metode Gauss-Seidel, yang diperkenalkan dalam Bagian 5.2, memberikan solusi yang konvergen untuk banyak masalah dalam CFD. Metode ini paling efektif ketika diperlukan pengurangan yang moderat pada residu, misalnya sebagai bagian dari solusi keadaan mantap yang dijelaskan di Bagian 5.12.

Ketika metode Gauss-Seidel memerlukan banyak iterasi (misalnya, lebih dari 10) untuk konvergen ke toleransi yang sesuai, metode alternatif mungkin lebih efisien. Metode penurunan menyediakan penyelesaian matriks alternatif yang sering digunakan dalam CFD.

Metode penurunan menggambarkan persamaan yang sedang diselesaikan sebagai masalah minimisasi. Ini ditunjukkan di bawah ini menggunakan persamaan matriks berbentuk 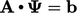dengan 2 nilai

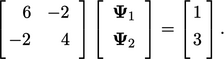2 3 2 3 2 3 6 2 1 1 4 5 4 5 = 4 5 : 2 4 2 3 \relax \special {t4ht=

(5.27)

Pada minimisasi ini, persamaannya disajikan dalam bentuk kuadratik; dalam notasi matriks, ini merupakan fungsi skalar dari bentuk

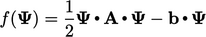1- f ( ) = 2 A b \relax \special {t4ht=

(5.28)

Bentuk kuadratik dari Persamaan (5.27) adalah:

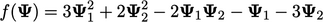f ( ) = 3 21 + 2 22 2 1 2 1 3 2 \relax \special {t4ht=

(5.29)

Gradien dari persamaan f(ψ) adalah:

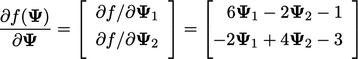2 3 2 3 @f-(--) 4 @f=@ 1 5 4 6 1 2 2 1 5 @ = @f=@ 2 = 2 1 + 4 2 3 \relax \special {t4ht=

(5.30)

Secara kritis, 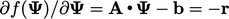, yaitu negatif dari vektor residu Persamaan (5.10), seperti yang diverifikasi oleh contoh model.

Menyamakan gradien dengan nol, 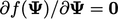, sesuai dengan minimum dalam fungsi kuadratik. Pada saat yang sama, itu adalah solusi untuk 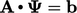.. Oleh karena itu, metode ini berkaitan dengan menemukan minimum dari bentuk kuadratik secara efisien.

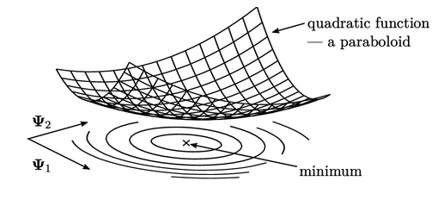
Untuk metode ini dapat berhasil, bentuk kuadratik harus memiliki nilai minimum, yang memerlukan agar A simetris dan positif-deﬁnit. Matriks positif-deﬁnit sulit untuk divisualisasikan, tetapi untuk fungsi 2-nilai, ini memastikan fungsi kuadratik adalah paraboloid.

Dominasi diagonal adalah kondisi konvergensi untuk metode Gauss-Seidel, yang dibahas di Bagian 5.3. Pentingnya, sebuah matriks simetris yang dominan secara diagonal, dan memiliki koefisien diagonal positif, juga positif-deﬁnit

Operasi matriks

Operasi ‘∙’ antara dua matriks kolom tunggal, misalnya , dalam Persamaan (5.28) direpresentasikan dalam notasi matriks oleh transpose 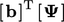. dalam teks lain. Untuk contoh dalam Persamaan (5.27), hal tersebut adalah:

2 3 T h i 1 b = [b ] [ ] = 1 3 4 2 5 = 1 + 3 2 \relax \special {t4ht=

(5.31)