5.15 Metode gradien konjugat

Metode gradien konjugat. Solusi untuk persamaan matriks 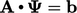dengan metode penurunan melibatkan menemukan nilai minimum dari persamaan dalam bentuk kuadratik. Hal ini dapat diilustrasikan menggunakan kontur dari paraboloid yang menggambarkan kuadratik untuk kasus dengan nilai 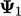dan .

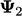Pencarian nilai minimum melibatkan serangkaian pembaruan pada ψ dalam bentuk

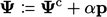$ℬ c + p \relax \special {t4ht=$

(5.32)

di mana 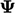adalah pembaruan berikutnya menggunakan nilai terbaru (saat ini) 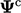. Vektor kolom P memberikan arah dari pencarian garis menuju nilai minimum; skalar α memberikan besarnya garis dalam arah tersebut

Penurunan tercepat

Cara intuitif untuk mencapai minimum adalah dengan mengikuti arah penurunan tercepat. Metode ini cukup sederhana karena arahnya didefinisikan oleh negatif dari gradien dari bentuk kuadratik 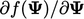yang merupakan residu

Jarak untuk “berjalan” adalah secara alami sampai titik terendah tercapai, yang sesuai dengan

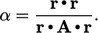r r = - ---- --: r A r \relax \special {t4ht=

(5.33)

Metode ini mencapai titik minimum sepanjang jalur zigzag di mana arah consecutive (berurutan) bersifat ortogonal. Arah-arah tersebut tidak berubah dan menghasilkan sejumlah langkah yang sangat pendek, semakin besar paraboloid meregang ke satu arah.

Arah konjugat

Metode gradien konjugat (CG) memilih arah pencarian yang konjugat dengan A. Ini berarti setiap arah baru p berkorespondensi dengan yang sebelumnya 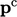, memenuhi

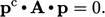$pc A p = 0: \relax \special {t4ht=$

(5.34)

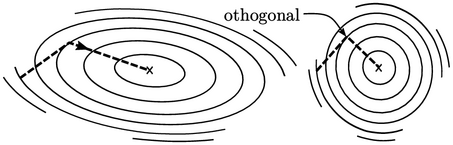
$PICT\relax \special {t4ht=$

Ini dapat diimajinasikan sebagai arah-arah yang bersifat ortogonal dengan peregangan dalam paraboloid dihilangkan. Untuk 2 nilai, CG menemukan minimum dalam 2 langkah, daripada beberapa langkah zigzag.

CG menyediakan dasar bagi penyelesaian matriks praktis untuk CFD, yang dijelaskan di Bagian 5.16. Untuk penjelasan terperinci tentang metode CG, lihat referensi di bawah ini.