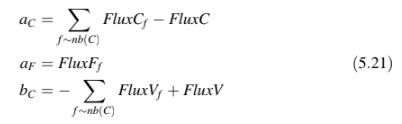5.2.4 Flux Linearization
Flux linearization. Seperti yang digambarkan secara skematis dalam Gambar 5.2a, aliran permukaan dapat dibagi menjadi bagian linear, yang bergantung pada nilai-nilai pada simpul yang melintasi permukaan dan bagian non-linear, yang mencakup bagian lain yang tidak dapat diungkapkan dalam hal
Persamaan yang dihasilkan dapat ditulis sebagai
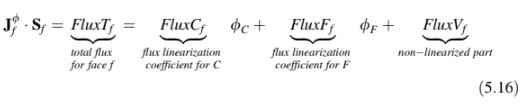
Dimana merupakan total fluks melalui permukaan
, dan didekomposisi menjadi tiga bagian. Dua istilah pertama mewakili kontribusi dari dua elemen yang berbagi permukaan dan ditulis melalui koefisien linearisasi
Istilah terakhir menggambarkan kontribusi non-linear yang tidak dapat diungkapkan dalam hal
dan diberikan oleh istilah non-linear
Nilai-nilai jelas bergantung pada
dan
istilah yang telah didiskritisasi dan skema yang digunakan untuk diskritisasi tersebut.
Linearisasi fluks ini diperoleh dengan mensubstitusi Persamaan (5.16) ke sisi kiri Persamaan (5.15). Mengulangi untuk semua permukaan sel menghasilkan
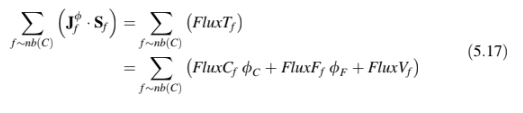
Linearisasi fluks volume dilakukan, seperti yang ditunjukkan dalam Gambar 5.3a, dengan mengekspresikannya sebagai fungsi linear dari nilai simpul elemen dan diberikan oleh.
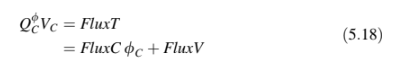
Dalam kasus istilah sumber yang konstan, fluks volume, yang mewakili sisi kanan dari Persamaan (5.15), menyusut menjadi.

Penggantian Persamaan (5.17) dan (5.18) dalam Persamaan (5.15) menghasilkan hubungan aljabar yang dicari, yaitu.
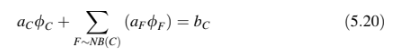
di mana hubungan antara koefisien persamaan dan koefisien linearisasi fluks diekspresikan sebagai.