
5.20 Pengendalian solusi sementara
Pengendalian solusi sementara. Kontrol tambahan berikut umumnya digunakan untuk solusi transien yang dijelaskan dalam Bagian 5.19:
- Sebuah loop iteratif di sekitar persamaan tekanan untuk memperbarui koreksi non-ortogonal;
- Sakelar on/off untuk prediktor momentum
Loop korektor non-orthogonal
Algoritma menyelesaikan persamaan tekanan, Pers. (5.19), yang mencakup diskritisasi dari istilah Laplacian 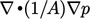 ,, sesuai dengan Bagian 3.7. Untuk jaringan komputasi dengan non-ortogonalitas yang signifikan, skema yang diperbaiki Pers. (3.7) harus diterapkan untuk menjaga akurasi yang memadai.
,, sesuai dengan Bagian 3.7. Untuk jaringan komputasi dengan non-ortogonalitas yang signifikan, skema yang diperbaiki Pers. (3.7) harus diterapkan untuk menjaga akurasi yang memadai.
Koreksi ini pada Laplacian tekanan dihitung menggunakan persamaan saat ini p, yang menghasilkan kontribusi eksplisit ke persamaan matriks. Persamaan tersebut dapat dibayangkan dengan koreksi eksplisit sebagai tambahan term 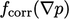 .
.
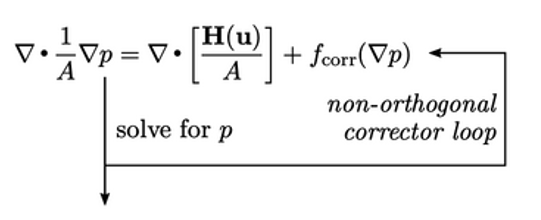
Untuk meningkatkan akurasi dalam setiap langkah waktu selama simulasi transien, 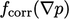 dapat dihitung ulang menggunakan p terbaru dan persamaan dipecahkan lagi.
dapat dihitung ulang menggunakan p terbaru dan persamaan dipecahkan lagi.
Akurasi dapat ditingkatkan dengan iterasi lebih lanjut, tetapi ini umumnya tidak disarankan karena biaya komputasi yang meningkat. Dengan persamaan tekanan dijumpai dua kali sebagai bagian dari loop PISO, dan dengan satu korektor setiap kali, matriks tekanan dipecahkan sebanyak 4 kali.
Mengatasi matriks tekanan itu mahal, sehingga setiap pengurangan dalam jumlah solusi disambut baik. Mengakui bahwa 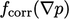 diperbarui sebagai bagian dari iterasi PISO dengan cara apa pun, strategi solusi alternatif menggunakan tanpa koreksi non-ortogonal tetapi menambahkan loop PISO tambahan, menyelesaikan persamaan tekanan sebanyak 3 kali.
diperbarui sebagai bagian dari iterasi PISO dengan cara apa pun, strategi solusi alternatif menggunakan tanpa koreksi non-ortogonal tetapi menambahkan loop PISO tambahan, menyelesaikan persamaan tekanan sebanyak 3 kali.
Menyelesaikan prediktor momentum
Algoritma transien pada halaman 385 termasuk prediktor momentum yang memberikan solusi awal untuk u, yang digunakan untuk mengevaluasi H(u) dalam persamaan tekanan. Solusi untuk p kemudian digantikan ke dalam korektor momentum yang menghitung u baru.
Karena u pada akhirnya dihitung ulang oleh korektor momentum — sebuah persamaan momentum dalam bentuk eksplisit — apakah perlu untuk menyelesaikan prediktor momentum sama sekali? Jawabannya adalah “tidak”, kecuali jika hal itu membuat solusi lebih konvergen, yang lebih mungkin terjadi untuk aliran berkecepatan tinggi yang lebih didominasi oleh pertukaran momentum daripada konservasi massa.
Oleh karena itu, algoritma transien seharusnya termasuk sakelar sederhana yang memungkinkan untuk mematikan langkah prediktor momentum. Sisanya dari algoritma tetap sama, dengan matriks momentum dibangun untuk memberikan H(u) dan A.
Dengan adanya sakelar ini, prediktor momentum kemudian dimatikan dalam banyak aplikasi, misalnya, aliran yang sangat kental. Dalam praktiknya, sering kali dimatikan untuk aliran yang lebih kompleks, misalnya, aliran multiphase, yang berada di luar lingkup buku ini.
