
5.3 KONVERGENSI
Konservasi. Metode Gauss-Seidel telah ditunjukkan dalam Bagian 5.2 menggunakan masalah contoh, Persamaan (5.2), yang konvergen dalam batas akurasi 0,2% dalam 9 kali iterasi solusi. Bagian ini membahas kriteria konvergensi suatu solusi.
Penjelasan paling mudah tentang konvergensi mempertimbangkan kesalahan 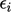 untuk setiap persamaan
untuk setiap persamaan 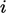 , yang didefinisikan di Bagian 5.2. Mengganti
, yang didefinisikan di Bagian 5.2. Mengganti 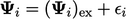 dalam setiap istilah dalam Persamaan (5.3), misalnya dalam Persamaan (5.3a), memberikan,
dalam setiap istilah dalam Persamaan (5.3), misalnya dalam Persamaan (5.3a), memberikan,
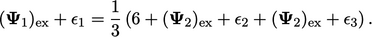 | (5.5) |
Karena 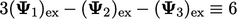 , Persamaan (5.5) menjadi lebih sederhana menjadi,
, Persamaan (5.5) menjadi lebih sederhana menjadi,
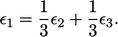 | (5.6) |
Besar kesalahan |𝜖_1 | setidaknya sebesar jumlah dari istilah-istilah di sisi kanan, namun lebih kecil jika tanda dari 𝜖_2 dan 𝜖_3 berbeda, yaitu
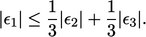 | (5.7) |
Mengulangi untuk Persamaan (5.3b) dan Persamaan (5.3c) memberikan:

Solusi bermula dari error inisial, 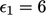 ,
, 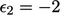 dan
dan 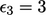 . Setelah satu sweep error (iterasi error) adalah
. Setelah satu sweep error (iterasi error) adalah 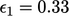 ,
, 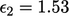 dan
dan 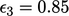
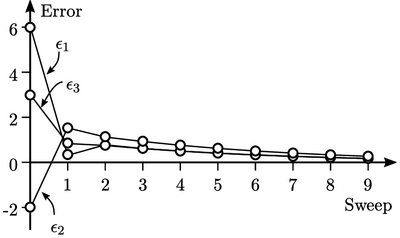
Kesalahan dengan cepat didistribusikan secara merata, sehingga 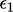 dan
dan 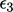 hampir identik pada langkah 2. Kesalahan terus berkurang sejak Persamaan (5.7) dan Persamaan (5.8) menjamin bahwa tidak ada kesalahan yang lebih besar dari rata-rata kesalahan lainnya.
hampir identik pada langkah 2. Kesalahan terus berkurang sejak Persamaan (5.7) dan Persamaan (5.8) menjamin bahwa tidak ada kesalahan yang lebih besar dari rata-rata kesalahan lainnya.
Kondisi Convergence
Perilaku masalah ini menunjukkan kondisi konvergensi untuk metode Gauss-Seidel: magnitudo koefisien diagonal dalam setiap baris matriks harus lebih besar atau sama dengan jumlah magnitudo koefisien lainnya dalam baris tersebut; dalam setidaknya satu baris, kondisi “lebih besar dari” harus terpenuhi.
Ini dikenal sebagai dominasi diagonal, yang merupakan kondisi yang cukup untuk konvergensi, dijelaskan secara matematis sebagai
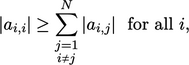 | (5.9) |
Di mana kondisi ‘>’ harus dipenuhi untuk setidaknya satu i . Deskripsi kondisi sebagai “cukup” berarti bahwa konvergensi dapat terjadi ketika kondisi tidak terpenuhi.
