5.4.2 Mean Value Approximation
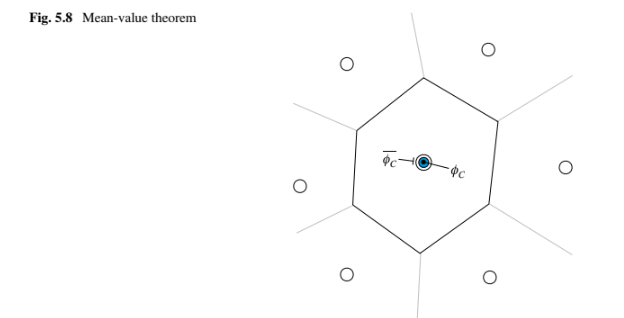
Mean value approximation. Akurasi dari pendekatan nilai rata-rata dapat diperoleh dengan mengintegrasikan variabel melalui sel dengan pusat massa C yang digambarkan dalam Gambar 5.8 dan menghasilkan
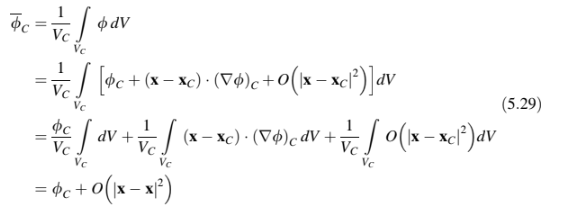
di mana adalah volume elemen. Istilah kedua sama dengan nol karena titik C adalah pusat massa elemen. Mengabaikan istilah terakhir dalam persamaan tersebut menghasilkan kesalahan orde 2, menunjukkan bahwa pendekatan nilai rata-rata adalah akurat hingga orde kedua.
Fluks konveksi di permukaan dari elemen C yang ditunjukkan dalam Gambar 5.9 dihitung sebagai:
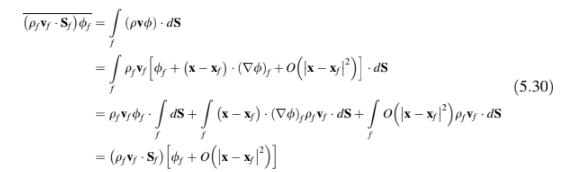
di mana lagi istilah kedua sama dengan nol karena adalah pusat massa dari permukaan elemen yang bersangkutan. Di sini subskrip
menunjukkan nilai variabel, dalam hal ini
di pusat massa permukaan dan S adalah vektor permukaan permukaan yang menunjuk ke luar.
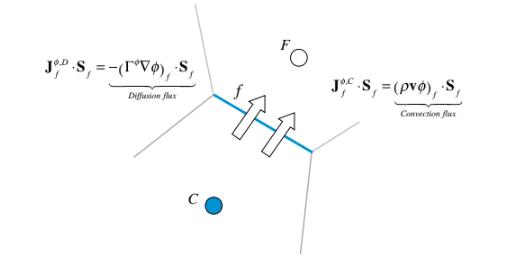
Untuk fluks difusi, dengan memotong istilah orde kedua dan yang lebih tinggi, dapat ditulis sebagai:
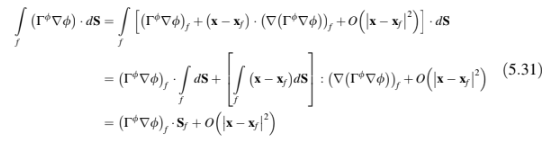
Oleh karena itu, untuk metode orde kedua, integral permukaan dan variasi Φ dalam elemen harus akurat hingga orde kedua. Akurasi orde yang lebih tinggi dapat dicapai dengan meningkatkan orde akurasi
integral permukaan atau profil yang diasumsikan untuk Φ. Salah satu metode yang dikembangkan oleh Lilek dan Peric [13] dalam dua dimensi menggunakan integral permukaan yang akurat hingga orde keempat, dievaluasi melalui aturan Simpson sebagai:
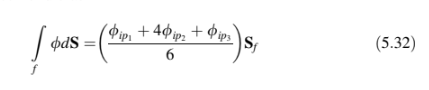
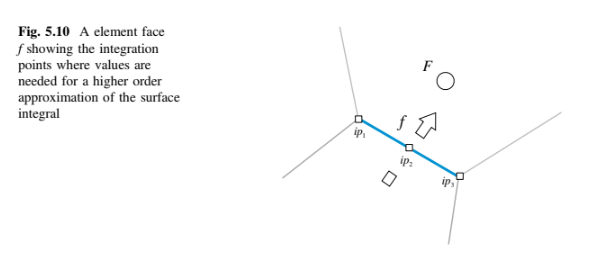
Seperti yang ditunjukkan dalam Gambar 5.10, untuk permukaan nilai
diperlukan di tiga titik integrasi, yaitu pusat massa permukaan
, dan sudut-sudut permukaan
Untuk memperoleh diskritisasi yang secara formal akurat hingga orde keempat, profil yang diasumsikan dari dalam
elemen juga harus akurat hingga orde keempat sehingga
Dalam hal ini, akurasi perhitungan gradien harus menjadi orde kedua atau lebih tinggi, sementara akurasi dari Hermitian harus menjadi orde pertama atau lebih tinggi.