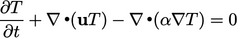5.5 Dominasi diagonal
Jika metode Gauss-Seidel diterapkan untuk menyelesaikan persamaan, solusi yang konvergen hanya dijamin jika kondisi dominasi diagonal dari Bagian 5.3 terpenuhi.
Kontribusi terhadap koefisien diagonal dan di luar diagonal dirangkum di bawah ini untuk setiap term dalam persamaan.

Istilah Laplacian 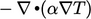 (perhatikan tanda), di-diskritisasi oleh Persamaan (3.2) dan Persamaan (3.5), memberikan kontribusi positif pada koefisien diagonal (yang terkait dengan
(perhatikan tanda), di-diskritisasi oleh Persamaan (3.2) dan Persamaan (3.5), memberikan kontribusi positif pada koefisien diagonal (yang terkait dengan 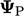 ) yang sama dengan jumlah magnitudo dari koefisien di luar diagonal yang negatif (untuk
) yang sama dengan jumlah magnitudo dari koefisien di luar diagonal yang negatif (untuk 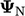 ).
).
Kontribusi dari istilah adveksi 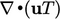 , yang dijelaskan oleh Persamaan (3.8), ditunjukkan di atas menggunakan skema interpolasi linear dari Persamaan (3.4). Tanda dari ϕ_f bergantung pada apakah aliran masuk atau keluar dari sel. Beberapa kontribusi pada koefisien di luar diagonal adalah negatif dan beberapa positif, dengan kontribusi diagonal cenderung menuju nol saat jaringan menjadi lebih teratur dan aliran menjadi lebih seragam.
, yang dijelaskan oleh Persamaan (3.8), ditunjukkan di atas menggunakan skema interpolasi linear dari Persamaan (3.4). Tanda dari ϕ_f bergantung pada apakah aliran masuk atau keluar dari sel. Beberapa kontribusi pada koefisien di luar diagonal adalah negatif dan beberapa positif, dengan kontribusi diagonal cenderung menuju nol saat jaringan menjadi lebih teratur dan aliran menjadi lebih seragam.
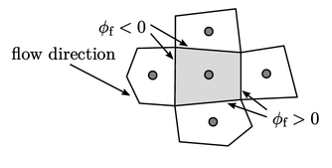
Adveksi dengan interpolasi linear menjaga kesetaraan diagonal sementara kontribusi positifnya pada koefisien di luar diagonal menyeimbangkan kontribusi negatif dari istilah Laplacian.
Namun, begitu kontribusi adveksi melebihi magnitudo kontribusi Laplacian, kesetaraan diagonal tidak tercapai. Hal ini terjadi Ketika 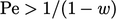 (= 2 untuk jaringan yang teratur), di mana “numerik” nomor Péclet
(= 2 untuk jaringan yang teratur), di mana “numerik” nomor Péclet 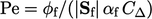 ditentukan pada permukaan sel berdasarkan definisinya di Bagian 2.21 dengan
ditentukan pada permukaan sel berdasarkan definisinya di Bagian 2.21 dengan 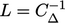 .
.
Kesetaraan diagonal tercapai dengan interpolasi hulu angin (upwind) dan dengan setiap skema yang memberikan koreksi eksplisit pada hulu angin, misalnya interpolasi linear hulu angin. Ini bersyarat pada kepuasan konservasi massa, seperti yang dibahas di Bagian 3.22. Jika massa tidak terjaga, skema adveksi yang terbatas, seperti yang dijelaskan dalam bagian tersebut, diperlukan untuk memastikan kesetaraan diagonal.
Turunan waktu 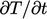 hanya meningkatkan koefisien diagonal saja, sehingga mendorong dominasi diagonal. Perlu dicatat bahwa kontribusi diagonal dari
hanya meningkatkan koefisien diagonal saja, sehingga mendorong dominasi diagonal. Perlu dicatat bahwa kontribusi diagonal dari 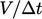 dari
dari 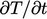 menjadi lebih besar dari pada
menjadi lebih besar dari pada 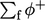 dari adveksi dengan hulu angin ketika
dari adveksi dengan hulu angin ketika 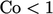 .
.
Secara ringkas, dominasi diagonal tidak dijamin karena kontribusi dari istilah adveksi.