5.6.7 Transportiveness
Transportiveness. Properti arah yang ditunjukkan oleh transportasi fluida sudah dikenal dengan baik dan ditandai oleh perubahan jenis persamaan skalar transportasi [Persamaan (5.2)], yang
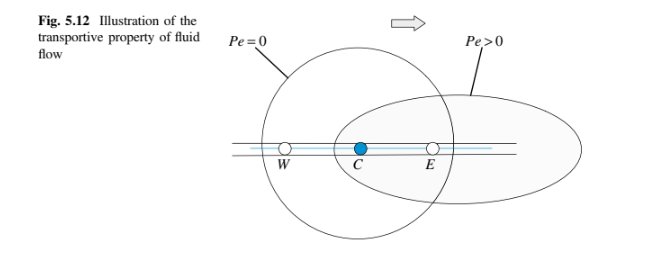
mungkin menjadi hiperbolik dalam kondisi tertentu. Implikasi pada persamaan volume terbatas, yang divisualisasikan dalam Gambar 5.12, dapat dijelaskan sebagai berikut. Jika terdapat sumber konstan dari Φ dalam suatu elemen C dalam suatu medan aliran dengan kecepatan dan difusivitas yang seragam, maka bentuk kontur Φ konstan akan dipengaruhi oleh rasio kekuatan konveksi terhadap difusi, yaitu, jumlah Péclet (Pe) yang didefinisikan sebagai
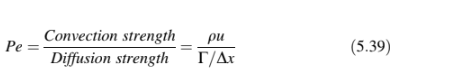
Berdasarkan Persamaan (5.39), kasus Pe = 0 menunjukkan bahwa transportasi Φ diatur oleh difusi, yang memiliki perilaku eliptis [8]. Dalam kasus ini, garis isoline Φ berbentuk lingkaran dan nilai Φ di C dipengaruhi oleh simpul-simpul sekitarnya W dan E (Gambar 5.12).
Meningkatnya efek konveksi (yaitu, meningkatnya Pe), kontur lingkaran menjadi berbentuk elips dan wilayah yang mempengaruhi nilai Φ di C bergeser ke arah aliran. Oleh karena itu, untuk aliran Pe tinggi, peristiwa di simpul C akan memiliki pengaruh lemah atau tidak ada pada simpul hulu, sementara simpul hilir akan sangat terpengaruh. Kegagalan untuk memperhatikan persyaratan ini dalam skema diskritisasi yang dipilih dapat menyebabkan solusi yang tidak stabil (yaitu, osilasi yang tidak fisik).
