9.2 Green-Gauss Gradient
Green-Gauss Gradient. Ini adalah salah satu metode yang paling banyak digunakan untuk menghitung gradien. Ini diperkenalkan dalam bab sebelumnya dan tidak akan diulang di sini. Sebaliknya, bentuk akhir dari persamaan akan diberikan dan beberapa metode tambahan untuk menghitung nilai wajah akan diperkenalkan. Seperti yang diturunkan dalam bab sebelumnya, gradien di pusat elemen C dengan volume (Gambar 8.8) dihitung sebagai
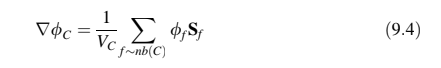
di mana merujuk pada sebuah wajah dan
pada vektor permukaannya. Nilai-nilai wajah
masih perlu didefinisikan sebelum rumus ini dapat digunakan. Dua pendekatan disajikan untuk menghitung
Satu adalah berbasis wajah dengan stencil umum yang kompak melibatkan tetangga wajah, dan yang kedua adalah berbasis vertex dengan stencil yang lebih besar melibatkan tetangga vertex. Jumlah sel dalam stencil yang diperluas ini sekitar dua kali lipat dari yang kompak.
Penggunaan stencil kompak menarik dengan metode implisit karena menghasilkan matriks Jacobian yang lebih kompak. Namun, stencil yang diperbesar membawa lebih banyak informasi ke dalam rekonstruksi, dan oleh karena itu diharapkan menjadi lebih akurat.
Metode 1: Stencil Kompak
Untuk sistem grid dua dan tiga dimensi yang ditunjukkan dalam Gambar 9.3a, b, masing-masing, sebuah pendekatan sederhana untuk menghitung adalah dengan menggunakan nilai rata-rata dari dua sel yang berbagi wajah. Dalam hal ini, nilai
dihitung sebagai
dimana adalah faktor bobot geometris yang sama dengan
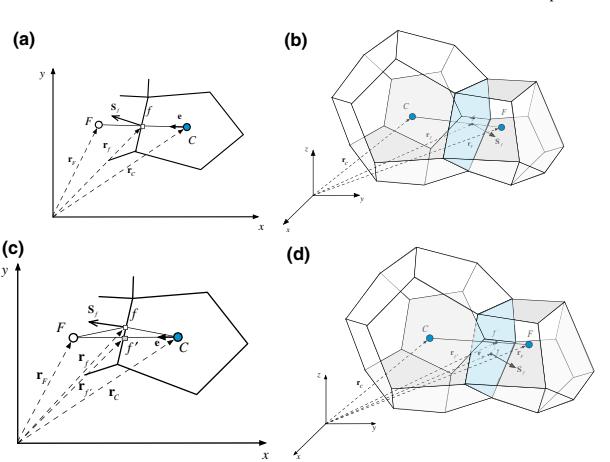
Fig. 9.3 Conjunctional face in a a two dimensional and b a three dimensional configuration;
non-conjunctional face in c a two dimensional and d a three dimensional configuration
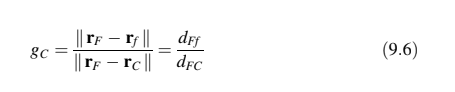
Di mana r menunjukkan vektor posisi dan d jarak antara dua titik. Ketika wajah berada di tengah-tengah antara dua pusat sel, ditemukan menjadi
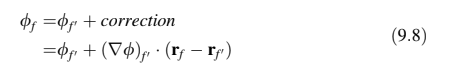
Pendekatan ini mudah diimplementasikan dalam situasi dua dan tiga dimensi, dan semua operasi yang terlibat didasarkan pada wajah, tidak memerlukan koneksi grid tambahan. Dari segi akurasi, hubungan di atas menghasilkan perkiraan orde kedua darihanya ketika segmen [CF] dan titik perpotongan wajah
bersamaan dengan pusat massa dari wajah
yaitu, dengan titik integrasi Gaussian
Dengan demikian, representasi gradien yang akurat hingga orde kedua umumnya tidak tercapai kecuali untuk kasus khusus di atas. Kondisi seperti ini biasanya tidak dipenuhi dengan sistem grid non-ortogonal terstruktur atau tidak terstruktur secara umum, seperti yang ditunjukkan untuk sistem grid dua dan tiga dimensi yang ditampilkan dalam Fig. 9.3c, d, masing-masing. Sebaliknya, kemiringan mesh (non-konjungtivitas) menyebabkan segmen [CF] dan permukaan
berpotongan pada.
Titik , berbeda dari pusat massa wajah
. Dalam hal ini, koreksi diperlukan untuk nilai
yang terinterpolasi untuk mendapatkan
. Persamaan koreksi diberikan oleh
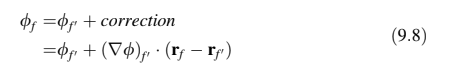
yang juga dapat ditulis dalam bentuk yang diperluas sebagai
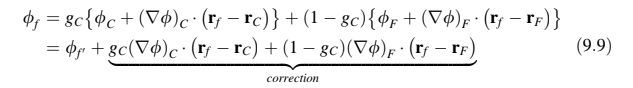
Karena tergantung pada
Persamaan (9.9) menunjukkan bahwa perkiraan yang diperbaiki dari gradien dapat diperoleh secara iteratif. Pada setiap iterasi, nilai rata-rata di wajah dihitung menggunakan gradien yang dihitung pada iterasi sebelumnya. Nilai-nilai wajah ini kemudian digunakan untuk menghitung perkiraan baru dari gradien. Melakukan jumlah iterasi yang berlebihan dapat menyebabkan osilasi dan biasanya tidak lebih dari dua iterasi dilakukan.
Dalam hal ini, perhitungan membutuhkan menemukan titik perpotongan
antara [CF] dan wajah
Untuk tujuan itu, tiga opsi akan dijelaskan.
Opsi 1: Dalam opsi ini, diambil sebagai perpotongan yang tepat antara [CF] dan wajah Sf dari vektor permukaan Sf. Dengan n menunjukkan vektor satuan permukaan (yaitu, n =
/
) dan e vektor satuan sepanjang CF (yaitu, e = CF / ||CF||), lokasi
(Gambar 9.3c, d) dapat ditemukan dengan memanfaatkan kondisi ortogonalitas yang ada antara n dan segmen
(yaitu, n normal terhadap wajah
yang berisi segmen
) untuk menulis
Selanjutnya, karena adalah titik pada CF, vektor
dapat diungkapkan dalam hal e sebagai
di mana k adalah jumlah skalar. Menggabungkan Persamaan (9.10) dan (9.11) menghasilkan

Dengan ditemukan,
dihitung sebagai
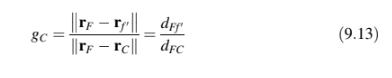
Langkah-langkah dalam prosedur perhitungan adalah sebagai berikut:
Selama iterasi pertama, hitung medan gradien di seluruh domain seperti berikut:
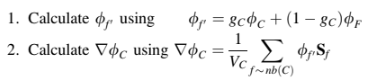
Mulai dari iterasi kedua dan seterusnya, perbaiki medan gradien sesuai dengan prosedur berikut:
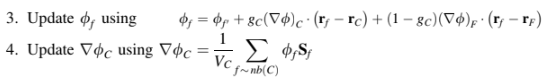
Opsi 2: Untuk dipilih berada di tengah segmen [CF] [Gambar 9.4a dalam dua dimensi dan Gambar 9.4b dalam tiga dimensi], persamaan menjadi lebih sederhana dan perhitungan medan gradien di atas domain berlanjut sebagai berikut:
Selama iterasi pertama, hitung medan gradien di seluruh domain sebagai berikut:
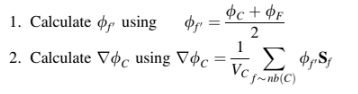
Mulai dari iterasi kedua dan seterusnya, perbaiki medan gradien sesuai dengan prosedur berikut:

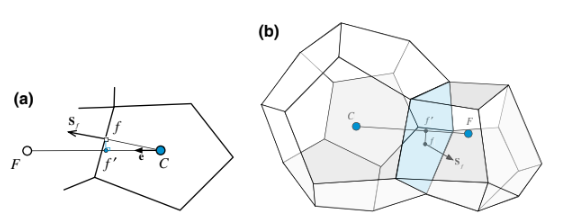
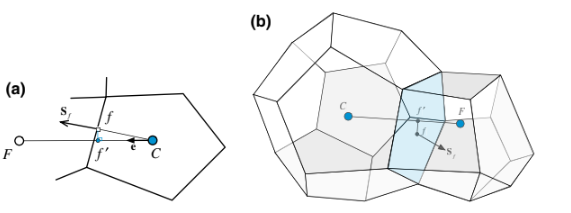
Opsi 3: Posisi dapat dipilih sedemikian rupa sehingga jarak
adalah yang paling pendek mungkin [Gambar 9.5a dalam dua dimensi dan Gambar 9.5b dalam tiga dimensi], yaitu,
tegak lurus terhadap [CF]. Hal ini menghasilkan perhitungan gradien yang lebih akurat selama iterasi pertama. Dalam hal ini,
dihitung dengan meminimalkan jarak antara
dan
. Secara umum,
dijelaskan oleh
di mana 0 < q < 1. Menyebut jarak
sebagai d, maka kuadratnya diperoleh sebagai
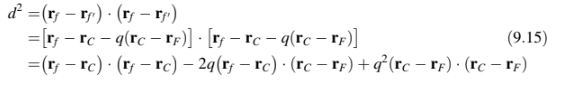
Meminimalkan fungsi terhadap q, menghasilkan
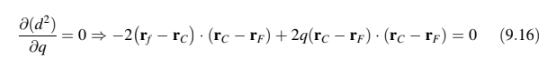
Dengan memecahkan, q diperoleh sebagai

Mengetahui nilai-nilai q, perhitungan gradien di atas domain dilanjutkan sebagai berikut:
Selama iterasi pertama, hitung medan gradien di seluruh domain sebagai berikut:
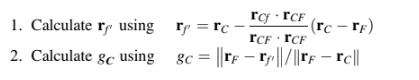

Mulai dari iterasi kedua dan seterusnya, perbaiki medan gradien sesuai dengan prosedur berikut:
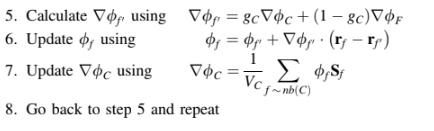
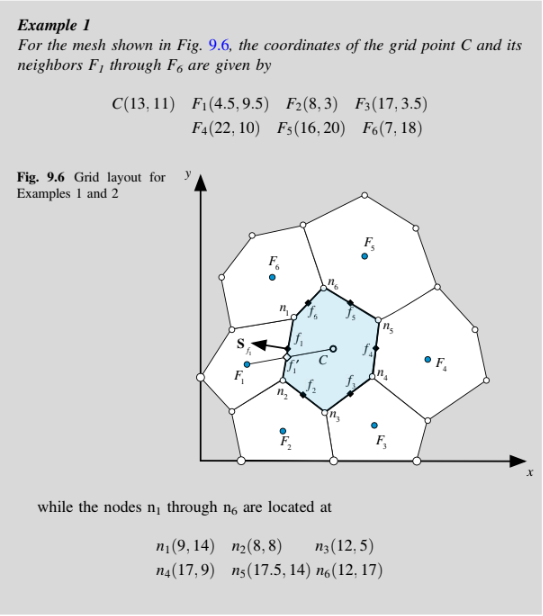



Nilai dari di pusat massa permukaan
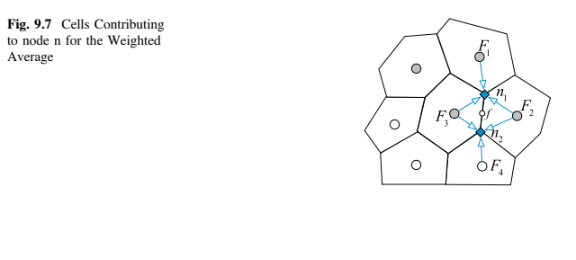
dapat dihitung sebagai rata-rata dari nilai-nilai di titik sudut yang menentukan permukaan. Ini memerlukan estimasi sifat-sifat di titik sudut. Sifat-sifat di simpul titik sudut dihitung menggunakan rata-rata tertimbang dari sifat-sifat di dalam sel-sel yang mengelilingi simpul tersebut. Gambar 9.7 menunjukkan sel-sel yang dipertimbangkan untuk rata-rata tertimbang dari sifat-sifat di simpul titik sudut
Bobot diambil sebagai invers dari jarak simpul sudut ke pusat sel. Persamaan yang dihasilkan untuk sifat-sifat di simpul-simpul sudut ditulis sebagai berikut:
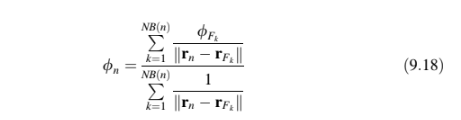
di mana n mengacu pada simpul sudut,mengacu pada simpul sel tetangga, NB(n) jumlah total simpul sel yang mengelilingi simpul sudut n, dan
merupakan jarak dari simpul sudut ke pusat massa sel tetangga.
Setelah nilai-nilai di simpul sudut ditemukan, nilai-nilai
di pusat massa permukaan dihitung diikuti dengan gradien di pusat massa kendali. Pada situasi dua dimensi,
dihitung sebagai.

Kemudian gradien di C ditemukan menggunakan
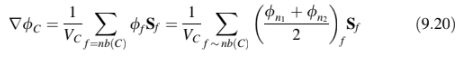
Dalam situasi tiga dimensi, perhitungannya sedikit lebih rumit karena jumlah simpul sudut wajah tergantung pada jenis elemen. Nilai /f ditemukan dari nilai-nilai di titik sudut menggunakan

where n represents the number of vertices of face Once the values
are cal-
culated, the gradient at C is computed using Eq. (9.4).
One of the disadvantages of this approach is that information from the wrong
side of the cell face also contributes to the weighted average values of the conserved
variables. This can be overcome by using upwind biased gradients as discussed by
Cabello [4]. The higher order calculations based on the upwind biased gradients,
however, have both higher memory overheads required to store the information
about the cells used for the upwind biased gradient calculation and increased coding
complexity.

