A Preliminary Derivation: The Central Difference(CD) Scheme
A preliminary derivation: the central difference (CD) scheme. Pada pandangan pertama, jawaban “yang jelas” akan menjadi profil interpolasi linear yang mirip dengan yang digunakan untuk istilah difusi. Oleh karena itu, nilai ϕ pada suatu wajah tertentu, misalnya wajah kanan e, akan dihitung sebagai
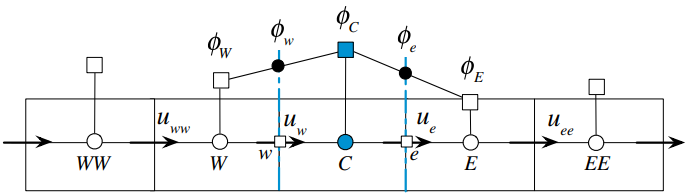
Gambar 11.3: Profil Skema Perbedaan Tengah
Di mana k0 dan k1 adalah konstan yang dievaluasi menggunakan dua simpul yang melintasi wajah e. Dengan demikian, menggunakan fakta bahwa ϕ = ϕE saat x = xE dan ϕ = ϕC saat x = xC, Persamaan (11.17) dievaluasi pada x = xe memberikan
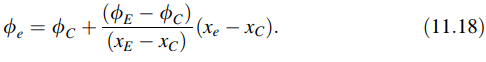
Ini pada dasarnya adalah skema perbedaan tengah yang dapat diperoleh melalui ekspansi deret Taylor di mana suku-suku yang melibatkan turunan orde kedua dan yang lebih tinggi diabaikan, yang berarti skema ini akurat orde kedua. Untuk grid seragam yang ditunjukkan dalam Gambar 11.3, Persamaan (11.18) menjadi

Oleh karena itu, setelah diskritisasi istilah difusi menggunakan profil linear (Gambar 11.3), suku dalam kurung siku pertama dari Persamaan (11.16) menjadi
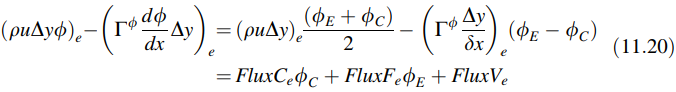
dimana
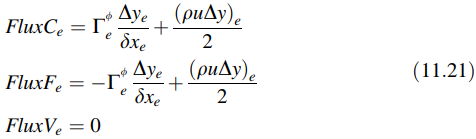
Ekspresi serupa untuk suku dalam kurung siku kedua dari Persamaan (11.16) juga dapat diturunkan dan diberikan oleh
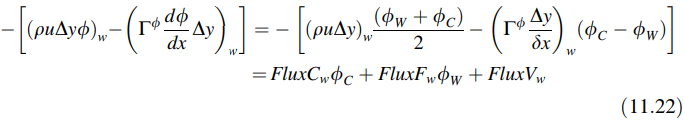
dimana sekarang
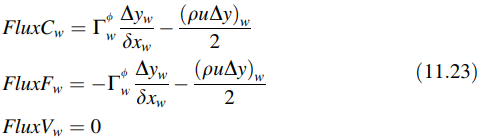
Substitusi nilai-nilai ini ke dalam persamaan konveksi-difusi menghasilkan
dimana
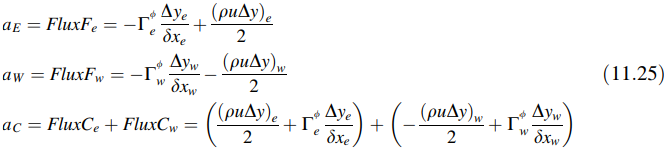
Karena masalahnya bersifat satu dimensi dan Δye = Δyw, maka tanpa kehilangan keumuman, dapat diatur sama dengan 1. Selain itu, dari kontinuitas, u adalah konstan dan dengan demikian ∂/∂x pada titik e dan ∂/∂x pada titik w adalah sama, sehingga (ρu∆y)e – (ρu∆y)w = 0. Dengan mengasumsikan koefisien difusi yang seragam, koefisien dari persamaan yang terdiskritisasi dapat disederhanakan menjadi
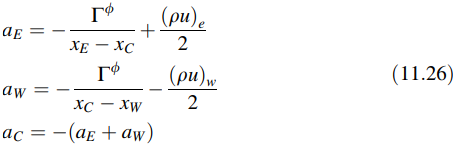
Dengan melakukan substitusi kembali ke Persamaan (11.24), nilai untuk ϕC ditemukan sebagai

Jika grid diasumsikan seragam, maka persamaan di atas dapat ditulis dalam istilah PeL sebagai
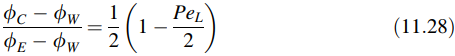
Di mana L adalah (xE – xW), yang merupakan ukuran dari dua elemen. Solusi analitis untuk masalah ini dapat diperoleh dari Persamaan (11.10) dengan mengatur (x – xW)/L menjadi 0.5 dan diberikan oleh

Dua solusi dibandingkan dalam Gambar 11.4 saat PeL bervariasi dari -10 hingga +10. Gambar 11.4 menunjukkan bahwa pada nilai PeL yang rendah, solusi numerik dan analitis sangat dekat satu sama lain.
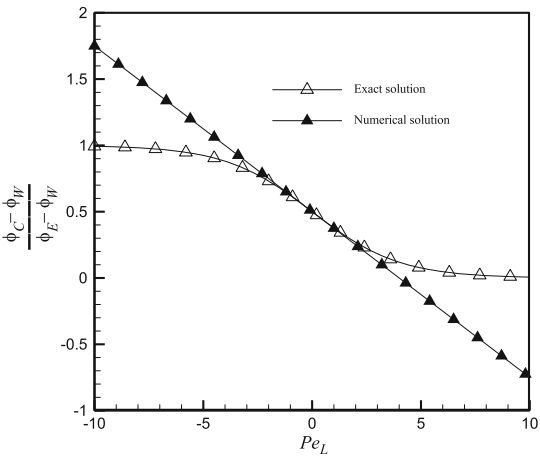
Gambar 11.4 Perbandingan solusi numerik (diperoleh dengan skema CD) dan analitis untuk masalah konveksi-difusi satu dimensi
Namun, saat PeL meningkat melebihi nilai tertentu, solusi numerik dengan skema perbedaan tengah (CD) secara signifikan menyimpang dari solusi analitis dan menjadi tidak terbatas mengalami perilaku yang tidak fisik. Sedangkan solusi analitis mendekati nilai 0 dan 1 secara asimtotik untuk nilai positif dan negatif dari PeL, masing-masing, solusi CD menurun secara linear dari +∞ ke −∞ saat PeL meningkat dari −∞ ke +∞. Solusi ini mengindikasikan bahwa beberapa asumsi yang digunakan dalam diskritisasi persamaan adalah tidak realistis atau tidak fisik. Apa penyebab dari perilaku ini?
Seperti yang digambarkan dalam Gambar 11.5, sementara difusi di titik C sama-sama dipengaruhi oleh kondisi hulu dan hilir dari C (Gambar 11.5a), proses adveksi adalah proses yang sangat berarah yang hanya mengangkut sifat-sifat dalam arah aliran (Gambar 11.5b). Oleh karena itu, aproksimasi profil linear, yang memberikan bobot yang sama pada simpul hulu dan hilir, adalah aproksimasi yang baik untuk istilah difusi (Gambar 11.5a). Namun, itu tidak dapat menggambarkan preferensi arah dari adveksi, untuk itu profil langkah lebih sesuai (Gambar 11.5b), dan merupakan penyebab masalah ini.
Zona pengaruh gabungan adveksi-difusi dan profil yang lebih relevan dalam kasus ini digambarkan secara skematis dalam Gambar 11.5c. Zona pengaruh ini mendekati wilayah difusi yang ditampilkan dalam Gambar 11.5a dan wilayah adveksi yang digambarkan dalam Gambar 11.5b pada nilai rendah dan tinggi dari angka Péclet, masing-masing.
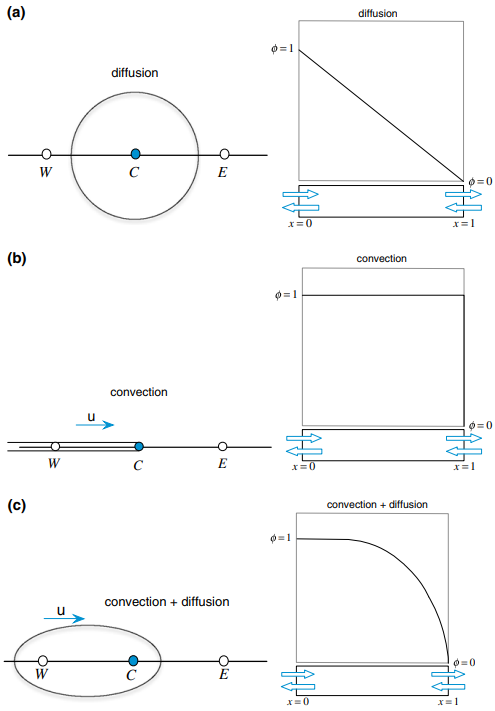
Gambar 11.5 Zona pengaruh dari a difusi, b adveksi, dan c istilah gabungan adveksi dan difusi serta solusi masalah yang diharapkan.
Oleh karena itu, selama difusi merupakan mekanisme transfer dominan, penggunaan profil linear menghasilkan hasil yang fisik. Namun, begitu adveksi mengatasi difusi, hasil yang tidak fisik diperoleh. Nilai angka Péclet di mana ini terjadi dapat dengan mudah dihitung. Dengan asumsi aliran bergerak ke arah x positif, perlu dicatat bahwa ada kemungkinan koefisien aE menjadi positif, sehingga menghasilkan hasil yang tidak fisik (jika aliran bergerak ke arah x negatif, maka aW mungkin menjadi positif) saat,
Mendefinisikan angka Péclet sel sebagai
yang untuk grid seragam adalah setengah dari PeL, maka Persamaan (11.30) dapat ditulis ulang sebagai
Oleh karena itu, untuk angka Péclet sel (Pe) yang lebih besar dari 2, proses diskritisasi menjadi tidak konsisten karena peningkatan nilai tetangga akan menyebabkan penurunan nilai di C. Ini pada gilirannya akan menyebabkan peningkatan lebih lanjut dalam nilai tetangga, dan kesalahan tersebut diperbesar.
Kondisi ini dapat dihindari dengan mengurangi ukuran grid sehingga angka Péclet sel lebih kecil dari 2. Namun, untuk banyak situasi praktis, peningkatan dalam kebutuhan penyimpanan dan komputasi mungkin terlalu besar untuk diatasi. Selain itu, untuk aliran yang murni terbawa (misalnya, aliran Euler), hal ini tidak mungkin dilakukan. Oleh karena itu, diperlukan suatu penanganan.
