10.2.13 Algoritma Matriks Tridiagonal (TDMA)
Algoritma Matriks TriDiagonal (TDMA), juga dikenal sebagai algoritma Thomas [5, 6], menyelesaikan sistem persamaan aljabar dengan matriks koefisien tridiagonal yang ditulis sebagai
Untuk tata letak grid yang diadopsi dalam buku ini, i merujuk pada lokasi titik grid yang ditunjukkan dalam Gambar 10.1.

Gambar 10.1 Susunan grid satu dimensi
Untuk i = 1, persamaan tersebut dapat digunakan untuk menyelesaikan dalam istilah
sebagai berikut:
Demikian pula untuk i = 2, Persamaan (10.29) dengan bantuan Persamaan (10.30) memungkinkan untuk mengekspresikan secara eksklusif dalam istilah
sebagai berikut:
Hal yang sama dapat diulang untuk hingga
menyarankan bahwa secara umum
dapat diekspresikan sebagai fungsi dari
sesuai dengan
Persamaan (10.32) untuk i − 1 bila digabungkan dengan Persamaan (10.29) menghasilkan
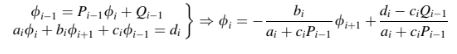
Dengan membandingkan Persamaan (10.32) dengan Persamaan (10.33), hubungan rekurensi berikut untuk Pi dan Qi ditemukan:
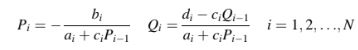
Untuk i = 1, nilai-nilai Pi dan Qi dihitung dari Persamaan (10.30) sebagai berikut
Untuk i = N, karena = 0 maka dapat disimpulkan hal berikut:
Algoritma solusi TDMA dapat disimpulkan sebagai berikut:

