Aliran Couette
Aliran Couette. Masalah plat yang bergerak menghasilkan syarat batas yang berbeda untuk kecepatan. Untuk kasus ini, kita menempatkan asal sistem koordinat di plat bawah dan menetapkan jarak antara dua plat sebagai b (lihat Gambar 6.32a). Dua konstanta c1 dan c2 dalam Persamaan 6.133 dapat ditentukan dari syarat batas tanpa selip, u=0 saat y=0 dan u=U saat y=b. Ini mengikuti bahwa c1 =0 dan c2 =U. Sehingga,
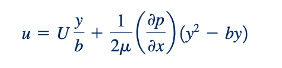
atau, dalam bentuk tak berdimensi,
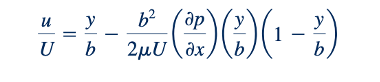
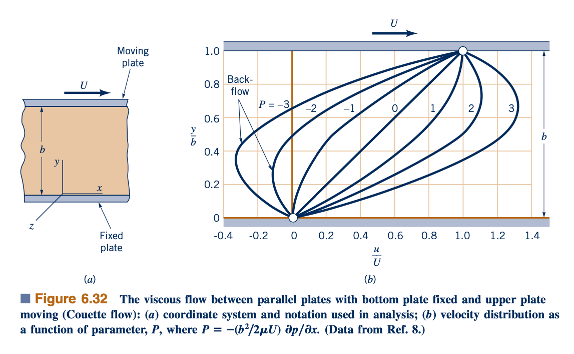

Profil kecepatan aktual akan tergantung pada parameter tak berdimensi
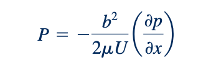
Beberapa profil ditunjukkan dalam Gambar 6.32b. Jenis aliran ini disebut aliran Couette.
Jenis aliran Couette yang paling sederhana adalah yang gradien tekanannya nol; artinya, gerakan fluida disebabkan oleh fluida yang ditarik oleh batas yang bergerak. Dalam hal ini, dengan gradien tekanan nol 𝜕𝑝/𝜕𝑥=0, Persamaan 6.140 hanya menyederhanakan menjadi
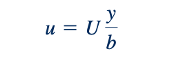
Ini mengindikasikan bahwa kecepatan bervariasi secara linear antara dua pelat seperti yang ditunjukkan dalam Gambar 6.31b untuk P = 0. Situasi ini akan didekati oleh aliran antara silinder berdekatan yang berkonsentrasi di mana satu silinder diam dan yang lainnya berputar dengan kecepatan sudut konstan, w. Seperti yang ditunjukkan dalam Gambar 6.33, aliran dalam bantalan jurnal yang tidak dimuat bisa didekati dengan aliran Couette sederhana ini jika lebar celah sangat kecil (yaitu r0 -ri ≪ ri). Dalam hal ini, U= ri w, b=ro -ri, dan tegangan geser yang menahan rotasi poros dapat dihitung secara sederhana sebagai 𝜏=𝜇𝑟𝑖𝜔/(𝑟𝑜−𝑟𝑖 ). Ketika bantalan dimuat (yaitu, gaya diterapkan tegak lurus terhadap sumbu rotasi), poros tidak akan tetap konsentris dengan rumah dan aliran tidak dapat dianggap sebagai aliran antara batas sejajar. Masalah seperti ini diatasi dalam teori pelumasan (lihat, misalnya, Ref. 9).


