Aliran di Sekitar Benda Terendam
Aliran di sekitar benda terendam. Model-model telah banyak digunakan untuk mempelajari karakteristik aliran yang terkait dengan benda yang sepenuhnya tenggelam dalam fluida yang bergerak. Contohnya termasuk aliran di sekitar pesawat terbang, mobil, bola golf, dan bangunan. Model-model ini biasanya diuji di terowongan angin seperti yang digambarkan dalam Gambar 7.6. Hukum-hukum pemodelan untuk masalah-masalah ini mirip dengan yang dijelaskan dalam bagian sebelumnya; yaitu, kesamaan geometri dan jumlah Reynolds diperlukan. Karena tidak ada antarmuka fluida, tegangan permukaan (dan oleh karena itu nomor Weber) tidak penting. Selain itu, gravitasi tidak akan memengaruhi pola aliran, sehingga nomor Froude tidak perlu dipertimbangkan. Nomor Mach akan penting untuk aliran berkecepatan tinggi di mana kompresibilitas menjadi faktor penting, tetapi untuk fluida inkompresibel (seperti cairan atau gas pada kecepatan relatif rendah), nomor Mach dapat diabaikan sebagai persyaratan kesamaan. Dalam hal ini, rumusan umum untuk masalah-masalah ini adalah
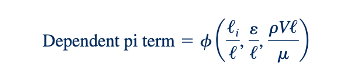
di mana ℓ adalah beberapa panjang karakteristik dari sistem dan ℓ mewakili panjang lain yang relevan, yaitu, ℓ adalah ketidakrataan relatif permukaan (atau permukaan), dan pVℓ/ 𝜇 adalah jumlah Reynolds. Seringkali, variabel tergantung yang menarik untuk jenis masalah ini adalah gaya gesek, 𝔇, yang terjadi pada benda, dan dalam situasi ini, pi term tergantung biasanya akan dinyatakan dalam bentuk koefisien gesek, CD, di mana

Faktor numerik, 1/2, adalah sembarang tetapi umumnya disertakan, dan ℓ2 biasanya diambil sebagai area representatif dari objek. Dengan demikian, studi gesek dapat dilakukan dengan formulasi


Jelas dari Persamaan 7.19 bahwa kesamaan geometris
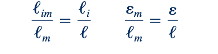
serta kesamaan jumlah Reynolds
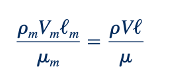
harus dipertahankan. Jika kondisi ini terpenuhi, maka

Atau

Pengukuran drag model, 𝔇m, kemudian dapat digunakan untuk memprediksi drag yang sesuai, 𝔇, pada prototipe dari hubungan ini.
Seperti yang dibahas dalam bagian sebelumnya, salah satu kesulitan umum dengan model terkait dengan persyaratan kesamaan nomor Reynolds yang menetapkan kecepatan model sebagai
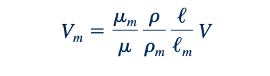
Atau
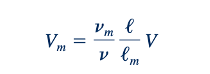
dimana vm/v adalah rasio viskositas kinematik. Jika fluida yang sama digunakan untuk model dan prototipe sehingga vm = v, maka

Dan, karena itu, kecepatan model yang diperlukan akan lebih tinggi daripada kecepatan prototipe untuk ℓ/ℓm lebih dari 1. Karena rasio ini seringkali relatif besar, nilai Vm yang diperlukan mungkin besar. Sebagai contoh, untuk skala panjang 1/10, dan kecepatan prototipe 50 mph, kecepatan model yang diperlukan adalah 10.500 mph. Ini adalah nilai yang tidak masuk akal tingginya untuk dicapai dengan cairan, dan untuk aliran gas hal ini akan berada dalam rentang di mana kekompresibilitas akan penting dalam model 1tetapi tidak pada prototipe2.
Sebagai alternatif, kita melihat dari Persamaan 7.21 bahwa Vm dapat dikurangi dengan menggunakan fluida yang berbeda dalam model sehingga vm /v < 1. Sebagai contoh, rasio viskositas kinematik air terhadap udara kira-kira 1 , sehingga jika fluida prototipe adalah udara, pengujian mungkin dilakukan pada model dengan menggunakan air. Hal ini akan mengurangi kecepatan model yang dibutuhkan, tetapi masih mungkin sulit untuk mencapai kecepatan yang diperlukan di fasilitas pengujian yang sesuai, seperti terowongan air.
Kemungkinan lain untuk pengujian terowongan angin adalah dengan meningkatkan tekanan udara di terowongan sehingga pm > p, sehingga mengurangi kecepatan model yang diperlukan seperti yang ditentukan oleh Persamaan 7.20. Viskositas fluida tidak sangat dipengaruhi oleh tekanan. Meskipun terowongan bertekanan telah digunakan, jelas lebih rumit dan mahal.
Kecepatan model yang diperlukan juga dapat dikurangi jika skala panjangnya sederhana; dengan kata lain, modelnya relatif besar. Untuk pengujian terowongan angin, ini memerlukan bagian uji yang besar yang sangat meningkatkan biaya fasilitas. Namun, terowongan angin besar yang cocok untuk menguji model atau prototipe yang sangat besar digunakan. Salah satu terowongan tersebut, yang terletak di Pusat Riset NASA Ames, Moffett Field, California, memiliki bagian uji yang berukuran 40 kaki kali 80 kaki dan dapat menampung kecepatan uji hingga 345 mph. Fasilitas pengujian yang besar dan mahal seperti itu jelas tidak layak untuk laboratorium universitas atau industri, sehingga sebagian besar pengujian model harus dilakukan dengan model yang relatif kecil.

Untungnya, dalam banyak situasi, karakteristik aliran tidak terlalu dipengaruhi oleh jumlah Reynolds di seluruh rentang operasi yang diminati. Dalam kasus-kasus ini, kita dapat menghindari persyaratan kesamaan yang cukup ketat dari pencocokan jumlah Reynolds. Untuk mengilustrasikan hal ini, pertimbangkan variasi koefisien drag dengan jumlah Reynolds untuk sebuah bola halus berdiameter d yang ditempatkan dalam aliran seragam dengan kecepatan pendekatan, V. Beberapa data khas ditunjukkan dalam Gambar 7.7. Kita melihat bahwa untuk jumlah Reynolds antara sekitar 103 dan 2 x 105, koefisien drag relatif konstan dan tidak terlalu bergantung pada nilai spesifik dari jumlah Reynolds. Dengan demikian, kesamaan jumlah Reynolds yang tepat tidak diperlukan dalam rentang ini. Untuk bentuk geometris lainnya, kita biasanya akan menemukan bahwa untuk jumlah Reynolds tinggi, gaya inersia mendominasi (daripada gaya viskositas), dan drag pada dasarnya independen dari jumlah Reynolds.

Satu hal menarik yang perlu diperhatikan dari Gambar 7.7 adalah penurunan tiba-tiba dalam koefisien drag di dekat jumlah Reynolds sekitar 3 x 105. Seperti yang dibahas dalam Bagian 9.3.3, hal ini disebabkan oleh perubahan kondisi aliran di dekat permukaan bola. Perubahan ini dipengaruhi oleh kekasaran permukaan dan, sebenarnya, koefisien drag untuk sebuah bola dengan permukaan yang "kasar" pada umumnya akan lebih rendah daripada bola halus untuk jumlah Reynolds tinggi. Misalnya, tonjolan pada bola golf digunakan untuk mengurangi drag dibandingkan dengan yang akan terjadi untuk bola golf yang halus. Meskipun ini tentunya menarik bagi penggila golf, ini juga penting bagi insinyur yang bertanggung jawab atas model aliran fluida, karena hal ini menekankan potensi pentingnya kekasaran permukaan. Namun, untuk benda yang cukup berbentuk sudut dengan sudut-sudut tajam, kekasaran permukaan aktual kemungkinan akan memainkan peran sekunder dibandingkan dengan fitur geometris utama dari benda tersebut.
Catatan terakhir terkait dengan Gambar 7.7 berkaitan dengan interpretasi data eksperimental saat plotting pi terms. Misalnya, jika p, 𝜇, dan d tetap konstan, maka peningkatan Re berasal dari peningkatan V. Secara intuitif, tampaknya secara umum jika V meningkat, drag akan meningkat. Namun, seperti yang ditunjukkan dalam gambar, koefisien drag umumnya menurun dengan peningkatan Re. Saat menginterpretasikan data, perlu diketahui apakah variabel tersebut berskala dimensi. Dalam hal ini, gaya drag fisik berkorelasi dengan koefisien drag dikalikan dengan kecepatan kuadrat. Dengan demikian, seperti yang ditunjukkan oleh gambar di margin, gaya drag, sesuai yang diharapkan, meningkat dengan peningkatan kecepatan. Pengecualian terjadi pada rentang jumlah Reynolds 2 x 10(5) < Re < 4 < 10(5)di mana koefisien drag menurun secara dramatis dengan peningkatan jumlah Reynolds (lihat Gambar 7.7). Fenomena ini dibahas dalam Bagian 9.3.
Untuk masalah yang melibatkan kecepatan tinggi di mana jumlah Mach lebih besar dari sekitar 0.3, pengaruh kompresibilitas, dan oleh karena itu jumlah Mach (atau jumlah Cauchy), menjadi signifikan. Dalam hal ini, kesamaan lengkap membutuhkan tidak hanya kesamaan geometris dan jumlah Reynolds tetapi juga kesamaan jumlah Mach sehingga

Persyaratan kesamaan ini, ketika digabungkan dengan persyaratan untuk kesamaan jumlah Reynolds (Eq. 7.21), menghasilkan

