Aliran melalui Saluran Tertutup
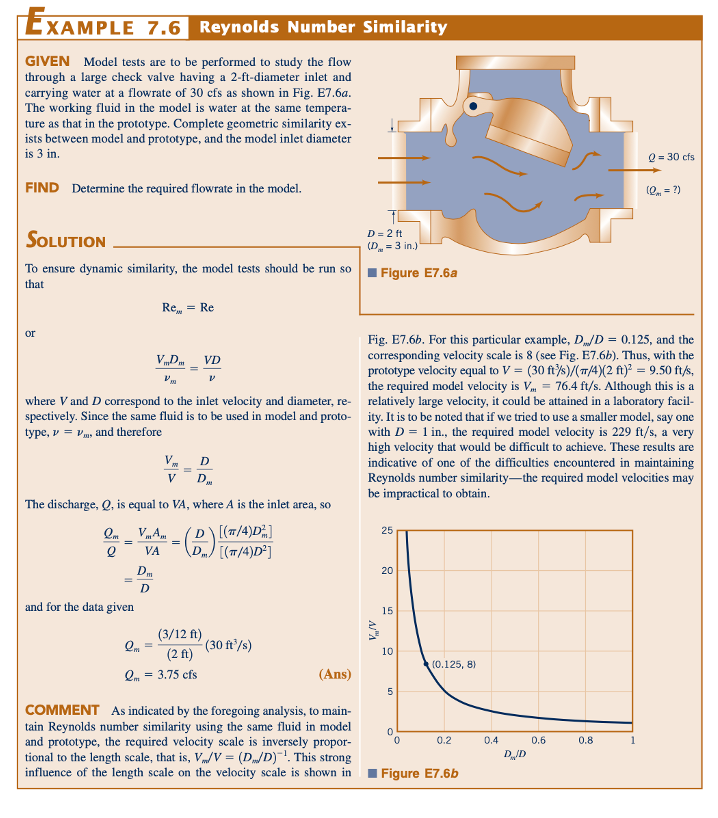
Aliran melalui saluran tertutup. Contoh umum dari jenis aliran ini termasuk aliran pipa dan aliran melalui katup, perlengkapan, dan perangkat pengukuran. Meskipun penampang saluran seringkali berbentuk bulat, mereka juga dapat memiliki bentuk lain dan mungkin mengandung pelebaran atau penyempitan. Karena tidak ada antarmuka fluida atau permukaan bebas, gaya dominan adalah inersial dan viskos sehingga jumlah Reynolds menjadi parameter kesamaan yang penting. Untuk angka Mach rendah (Ma ≤ 0,32), efek kompresibilitas biasanya diabaikan baik untuk aliran cairan maupun gas. Untuk jenis masalah ini, kesamaan geometris antara model dan prototipe harus dipertahankan. Secara umum, karakteristik geometris dapat dijelaskan oleh serangkaian panjang, ℓ1, ℓ2, ℓ3, ..., ℓi, dan ℓ, di mana ℓ adalah dimensi panjang tertentu untuk sistem tersebut. Serangkaian istilah panjang ini menghasilkan set kelompok pi yang berbentuk
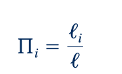
di mana i adalah 1, 2, ..., dan seterusnya. Selain dari geometri dasar sistem, kekasaran permukaan internal yang berkontak dengan fluida juga mungkin penting. Jika tinggi rata-rata elemen kekasaran permukaan didefinisikan sebagai 𝜀, maka kelompok pi yang mewakili kekasaran akan menjadi 𝜀/ℓ. Parameter ini menunjukkan bahwa untuk kesamaan geometris yang lengkap, kekasaran permukaan juga harus disesuaikan. Perlu diperhatikan bahwa hal ini menyiratkan bahwa untuk skala panjang kurang dari 1, permukaan model harus lebih halus daripada yang ada di prototipe karena 𝜀m =𝜆ℓ 𝜀. Untuk mempersulit masalah, pola elemen kekasaran dalam model dan prototipe juga harus serupa. Ini adalah kondisi yang hampir tidak mungkin dipenuhi dengan tepat. Untungnya, dalam beberapa masalah, kekasaran permukaan tidak berpengaruh.Peran kecil dan dapat diabaikan. Namun, dalam masalah lain (seperti aliran turbulen melalui pipa), kekasaran dapat menjadi sangat penting.
Dari pembahasan ini, dapat disimpulkan bahwa untuk aliran dalam saluran tertutup pada bilangan Mach rendah, setiap kelompok pi yang tergantung (yang mengandung variabel tertentu yang diminati, seperti penurunan tekanan) dapat diekspresikan sebagai

Ini adalah formulasi umum untuk jenis masalah ini. Dua kelompok pi pertama di sisi kanan Persamaan 7.16 mengarah pada persyaratan kesamaan geometris sehingga
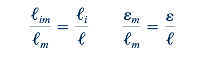
Atau
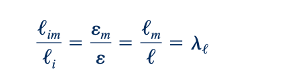
Hasil ini menunjukkan bahwa peneliti bebas memilih skala panjang, 𝜆ℓ, tetapi setelah skala ini dipilih, semua panjang lain yang relevan harus diubah skala dengan rasio yang sama.
Persyaratan kesamaan tambahan timbul dari kesetaraan nomor Reynolds
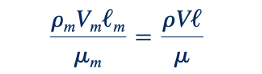
Dari kondisi ini, skala kecepatan ditetapkan sehingga
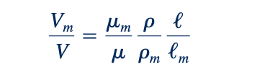
dan nilai sebenarnya dari skala kecepatan tergantung pada skala viskositas dan densitas, serta skala panjang. Berbagai fluida dapat digunakan dalam model dan prototype. Namun, jika fluida yang sama digunakan dengan (𝜇m =𝜇 dan pm=p) , maka

Dengan demikian, Vm adalah proporsional dengan Vm = 𝜆ℓ, yang menunjukkan bahwa kecepatan fluida dalam model akan lebih besar daripada dalam prototype untuk setiap skala panjang kurang dari 1. Karena skala panjang biasanya jauh lebih kecil dari kesatuan, kesamaan jumlah Reynolds mungkin sulit dicapai karena kecepatan model yang besar yang diperlukan.
Dengan persyaratan kesamaan ini terpenuhi, maka term pi tergantung akan sama dalam model dan prototype. Sebagai contoh, jika variabel tergantung yang diminati adalah perbedaan tekanan, Δp, antara dua titik sepanjang saluran tertutup, maka term pi tergantung bisa diungkapkan sebagai:
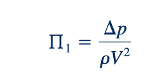
Penurunan tekanan pada prototipe kemudian dapat diperoleh dari hubungan:
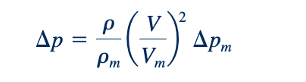
sehingga dari selisih tekanan yang diukur di model, ¢pm, perbedaan tekanan yang sesuai untuk prototipe dapat diprediksi. Perhatikan bahwa secara umum Δp ≠ Δpm.