Aliran Saluran Area Konstan Tanpa Gesekan dengan Perpindahan Panas (Aliran Rayleigh)
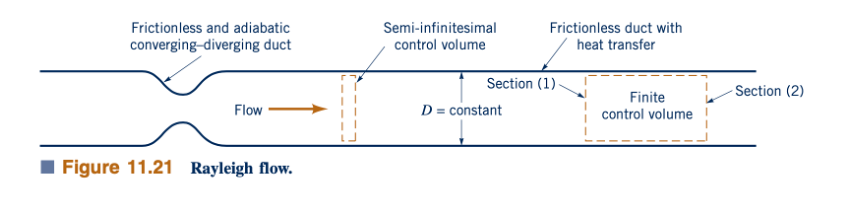
Aliran saluran area konstan tanpa gesekan perpindahan panas (Aliran Rayleigh). Pertimbangkan aliran ideal gas yang mantap, satu dimensi, dan bebas gesekan melalui saluran area tetap dengan transfer panas yang diilustrasikan dalam Gambar 11.21. Ini adalah aliran Rayleigh. Penerapan persamaan momentum linear (Eq. 5.222) pada aliran Rayleigh melalui volume kontrol yang terbatas seperti yang digambarkan dalam Gambar 11.21 menghasilkan persamaan:

Atau

Penggunaan persamaan keadaan gas ideal (Eq. 11.12) dalam Eq. 11.110 menghasilkan:

Karena luas penampang aliran tetap untuk aliran Rayleigh, dari persamaan kontinuitas (Eq. 11.402) kita menyimpulkan bahwa:

Untuk aliran Rayleigh yang diberikan, konstanta dalam Persamaan 11.111, produk densitas–kecepatan, pV, dan konstanta gas ideal semuanya tetap. Oleh karena itu, Persamaan 11.111 dapat digunakan untuk menentukan nilai suhu fluida yang sesuai dengan tekanan lokal dalam aliran Rayleigh.
Untuk membuat diagram suhu–entropi untuk aliran Rayleigh yang diberikan, kita dapat menggunakan Eq. 11.76, yang dikembangkan sebelumnya dari hubungan T ds kedua. Persamaan 11.111 dan 11.76 dapat dipecahkan secara bersamaan untuk mendapatkan kurva yang digambarkan dalam Gambar 11.22. Kurva seperti yang ada di Gambar 11.22 disebut garis Rayleigh.


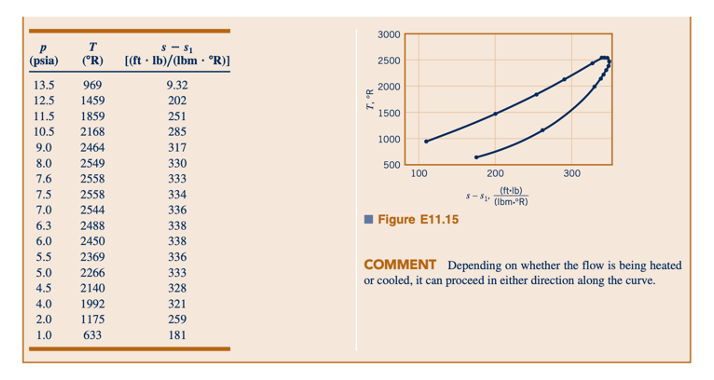
Pada titik a pada garis Rayleigh dari Gambar 11.22, ds/dT = 0. Untuk menentukan arti fisik dari titik a, kita analisis lebih lanjut beberapa persamaan yang mengatur. Dengan diferensiasi persamaan momentum linier untuk aliran Rayleigh (Eq. 11.110), kita dapatkan
Atau

Gabungan Eq. 11.112 dengan persamaan kedua T ds (Eq. 11.182) menghasilkan
Untuk gas ideal (Eq. 11.72), dh =cp dT. Dengan demikian, substitusi Eq. 11.7 ke Eq. 11.113 memberikan:

Atau
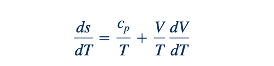
Konsolidasi dari Eqs. 11.114, 11.112 (persamaan momentum linier), 11.1, 11.77 (persamaan keadaan yang diferensiasi), dan 11.79 (kontinuitas) menghasilkan:

Oleh karena itu, pada titik a di mana ds/dT sama dengan nol, Eq. 11.115 mengungkapkan bahwa:
Perbandingan Eqs. 11.116 dan 11.36 memberi tahu kita bahwa Mach number di titik a sama dengan 1,
Pada titik b pada garis Rayleigh di Fig. 11.22, dT/ds = 0. Dari Persamaan 11.115, kita dapatkan bahwa relasi antara perubahan entropi terhadap perubahan suhu adalah negatif.
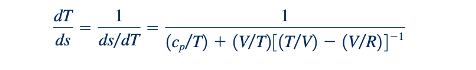
yang untuk dT/ds = 0 (titik b) memberikan

Aliran pada titik b adalah subsonik (Ma_b < 1,02). Ingat bahwa k > 1 untuk setiap gas.
Untuk mempelajari lebih lanjut tentang aliran Rayleigh, kita perlu mempertimbangkan persamaan energi selain dari persamaan yang sudah digunakan. Penerapan persamaan energi (Eq. 5.692) pada aliran Rayleigh melalui volume kontrol terbatas pada Gambar 11.21 menghasilkan:

atau dalam bentuk diferensial untuk aliran Rayleigh melalui volume kontrol semi-infinitesimal pada Gambar 11.21:

di mana 𝛿q adalah transfer panas per unit massa fluida dalam volume kontrol semi-infinitesimal.
Dengan menggunakan dh=cp dT=RkdT /(k-1), kita dapatkan
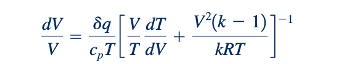
Maka, dengan menggabungkan Persamaan 11.36 (kecepatan suara gas ideal), 11.46 (bilangan Mach), 11.1 dan 11.77 (persamaan keadaan gas ideal), 11.79 (kontinuitas), dan 11.112 (momentum linear) dengan Persamaan 11.120 (energi), kita dapatkan
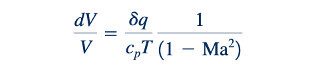
Dengan bantuan Persamaan 11.121, kita jelas melihat bahwa ketika aliran Rayleigh bersubsonik (Ma 0) meningkatkan kecepatan fluida sedangkan pendinginan fluida (𝛿q 1), pemanasan fluida mengurangi kecepatan fluida dan pendinginan fluida meningkatkan kecepatan fluida.
Hukum kedua termodinamika menyatakan bahwa, berdasarkan pengalaman, entropi meningkat dengan pemanasan dan menurun dengan pendinginan. Dengan wawasan tambahan yang diberikan oleh prinsip pelestarian energi dan hukum kedua termodinamika, kita dapat mengatakan lebih banyak tentang garis Rayleigh dalam Gambar 11.22. Ringkasan tentang aspek kualitatif dari aliran Rayleigh diuraikan dalam Tabel 11.2 dan Gambar 11.23. Pada bagian atas garis, yang mencakup titik b, aliran bersubsonik. Memanaskan fluida mengakibatkan percepatan aliran hingga mencapai kecepatan Mach maksimum pada titik a. Perhatikan bahwa di antara titik b dan a sepanjang garis Rayleigh, memanaskan fluida menghasilkan penurunan suhu dan mendinginkan fluida menyebabkan peningkatan suhu. Trend ini tidak mengejutkan jika kita mempertimbangkan perubahan suhu stagnasi dan kecepatan fluida yang terjadi antara titik a dan b ketika fluida dipanaskan atau didinginkan. Di sepanjang bagian bawah kurva Rayleigh, aliran bersupersonik. Aliran Rayleigh mungkin atau mungkin tidak tercekik. Jumlah pemanasan atau pendinginan yang terlibat menentukan apa yang akan terjadi dalam suatu situasi tertentu. Seperti halnya aliran Fanno, decelerasi tiba-tiba dari aliran supersonik menjadi aliran subsonik melintasi gelombang kejut normal juga dapat terjadi dalam aliran Rayleigh.


Untuk mengkuantifikasi perilaku aliran Rayleigh, kita perlu mengembangkan bentuk-bentuk yang sesuai dari persamaan-persamaan yang mengaturnya. Kita memilih untuk menggunakan keadaan fluida aliran Rayleigh di titik a pada Gambar 11.22 sebagai keadaan referensi. Seperti yang ditunjukkan sebelumnya, Mach number di titik a adalah 1. Meskipun aliran Rayleigh yang dipertimbangkan mungkin tidak tercekik dan keadaan a tidak dicapai oleh aliran, keadaan referensi ini berguna.
Jika kita menerapkan persamaan momentum linear (Persamaan 11.110) pada aliran Rayleigh antara bagian hulu dan bagian, yang sesungguhnya atau dibayangkan, di mana keadaan a tercapai, kita mendapatkan:

Atau

Dengan mensubstitusi persamaan keadaan gas ideal (Persamaan 11.12) ke dalam Persamaan 11.122 dan memanfaatkan persamaan kecepatan suara gas ideal (Persamaan 11.362) serta definisi Mach number (Persamaan 11.462), kita mendapatkan:

Hubungan ini digambarkan dalam margin untuk udara.
Dari persamaan keadaan gas ideal (Persamaan 11.12), kita menyimpulkan bahwa

Konservasi massa (Persamaan 11.402) dengan A yang konstan memberikan
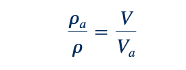

yang saat digabungkan dengan Persamaan 11.36 (kecepatan bunyi gas ideal) dan 11.46 (definisi bilangan Mach) menghasilkan

Kombinasi Persamaan 11.124 dan 11.126 menghasilkan
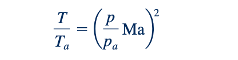
yang saat digabungkan dengan Persamaan 11.123 memberikan
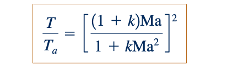

Dari Persamaan 11.125, 11.126, dan 11.128, kita melihat bahwa


Hubungan ini digambarkan di pinggir halaman untuk udara.
Persamaan energi (Persamaan 5.69) memberi tahu kita bahwa karena adanya transfer panas dalam aliran Rayleigh, suhu stagnasi bervariasi. Kami mencatat bahwa
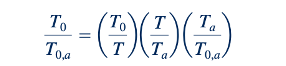
Kita dapat menggunakan Persamaan 11.56 (yang dikembangkan sebelumnya untuk aliran ideal gas isentropik dan stabil) untuk mengevaluasi T0/T dan Ta/T0,a karena kedua rasio suhu ini, sesuai dengan definisi dari keadaan stagnasi, melibatkan proses isentropik. Persamaan 11.128 dapat digunakan untuk T/Ta. Dengan demikian, dengan menggabungkan Persamaan 11.130, 11.56, dan 11.128, kita mendapatkan
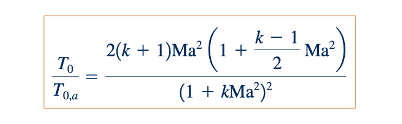

Hubungan ini digambarkan di pinggiran halaman untuk udara.
Terakhir, kita perhatikan bahwa
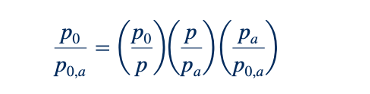
Kita dapat menggunakan Persamaan 11.59 yang dikembangkan sebelumnya untuk aliran gas ideal isentropik dan tetap dalam menghitung p0/p dan pa/p0,a karena kedua rasio tekanan tersebut, menurut definisi, melibatkan proses isentropik. Persamaan 11.123 dapat digunakan untuk p/pa. Bersama-sama, Persamaan 11.59, 11.123, dan 11.132 memberikan

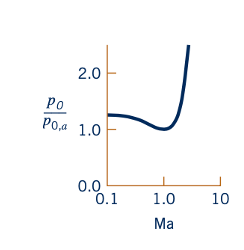
Hubungan ini digambarkan di pinggir untuk udara.
Nilai-nilai dari p/pa, T/Ta, r/ra, V/Va, dan p0/pa0 diplot dalam Fig. D.3 di Lampiran D sebagai fungsi dari jumlah Mach untuk aliran Rayleigh dari udara (k = 1,42). Nilai-nilai dalam Fig. D.3 dihitung dari Persamaan 11.123, 11.128, 11.129, 11.131, dan 11.133. Kebergunaan dari Fig. D.3 diilustrasikan dalam Contoh 11.16.
Lihat Ref. 7 untuk perlakuan yang lebih lanjut mengenai aliran internal dengan transfer panas.


