Aliran Saluran Konvergen–Divergen
Aliran saluran konvergen-divergen. Dalam bagian sebelumnya, kita membahas variasi densitas dan kecepatan dari aliran isentropis dan stabil dari gas ideal melalui saluran yang variabel luasnya. Sekarang kita akan mengembangkan persamaan yang membantu kita menentukan bagaimana properti aliran penting lainnya bervariasi dalam aliran-aliran ini.
Menggunakan kondisi stagnasi dari fluida sebagai kondisi referensi untuk perhitungan aliran kompresibel sangat nyaman. Kondisi stagnasi terkait dengan kecepatan aliran nol dan nilai entropi yang sesuai dengan entropi dari fluida yang mengalir. Subskrip 0 digunakan untuk menunjukkan kondisi stagnasi. Dengan demikian, suhu dan tekanan stagnasi adalah T0 dan p0. Misalnya, jika fluida yang mengalir melalui saluran yang menyempit-melebar dari Gambar 11.6a diambil secara isentropis dari atmosfer, tekanan dan suhu atmosfer akan mewakili kondisi stagnasi dari fluida yang mengalir. Kondisi stagnasi juga dapat dicapai dengan menurunkan secara isentropis kecepatan aliran menjadi nol. Ini dapat dilakukan dengan menggunakan saluran yang menyempit untuk aliran Subsonic atau saluran yang menyempit-melebar untuk aliran Supersonic. Juga, seperti yang dibahas sebelumnya dalam Bab 3, perlambatan secara hampir isentropis dapat dicapai dengan tabung Pitot-static (lihat Gambar 3.6). Dengan demikian, mungkin untuk mengukur, dengan hanya sedikit ketidakpastian, nilai tekanan stagnasi, p0, dan suhu stagnasi, T0, dari sebuah fluida yang mengalir.
Pada Bagian 11.1, kita menunjukkan bahwa untuk aliran isentropis dari gas ideal (lihat Pers. 11.25)

Persamaan gerak dalam arah sepanjang aliran untuk aliran yang mantap dan bebas gesekan (Pers. 11.41) dapat diekspresikan untuk gas ideal sebagai

karena istilah energi potensial, 𝛾 dz, dapat dianggap sangat kecil dibandingkan dengan istilah lain yang terlibat.
Dengan menggabungkan Persamaan 11.25 ke dalam Persamaan 11.51, kita mendapatkan
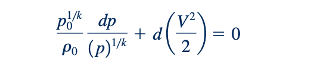
Pertimbangkan aliran ideal gas yang stabil, satu dimensi, isentropik dengan cp dan cv konstan melalui nosel yang berkonvergensi-membelok dari Gambar 11.6a. Persamaan 11.52 berlaku untuk aliran ini dan dapat diintegrasikan antara keadaan stagnasi umum dari fluida yang mengalir ke keadaan gas di lokasi mana pun dalam saluran berkonvergensi-membelok untuk memberikan
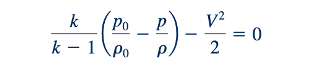
Dengan menggunakan persamaan keadaan gas ideal (Eq. 11.12) dengan Eq. 11.53, kita dapatkan
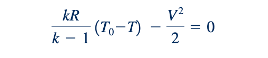
Menarik untuk dicatat bahwa dengan menggabungkan Persamaan 11.14 dan 11.54 menghasilkan
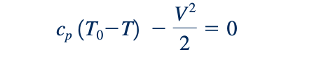
yang, ketika digabungkan dengan Persamaan 11.9, menghasilkan
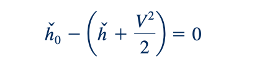
di mana h0 adalah entalpi stagnasi. Jika Persamaan energi aliran yang mantap 1Eq. 5.692 diterapkan pada situasi aliran yang sedang kita pertimbangkan saat ini, persamaan yang dihasilkan akan identik dengan Persamaan 11.55. Selanjutnya, kita menyimpulkan bahwa entalpi stagnasi konstan. Prinsip-prinsip kekekalan momentum dan energi mengarah pada persamaan yang sama (Eq. 11.55) untuk aliran isentropik mantap.
Definisi Mach number (Eq. 11.46) dan hubungan kecepatan suara untuk gas ideal (Eq. 11.36) dapat digabungkan dengan Persamaan 11.54 untuk menghasilkan
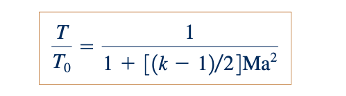
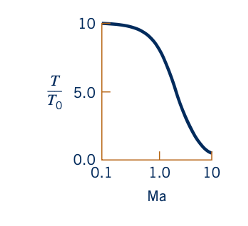
Dengan Persamaan 11.56, kita dapat menghitung suhu gas ideal di mana pun di saluran konvergen-divergen dari Gambar 11.6a jika aliran adalah stabil, satu dimensi, dan isentropik, asalkan kita mengetahui nilai Mach number lokal dan suhu stagnasi.
Kita juga dapat mengembangkan persamaan untuk variasi tekanan. Karena p/ρ=RT, maka
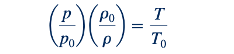
Dari Persamaan 11.57 dan 11.25, kita dapatkan
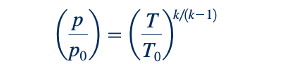
Gabungan Persamaan 11.58 dan 11.56 menghasilkan
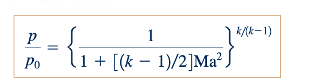
Untuk variasi densitas, kita gabungkan Persamaan 11.56, 11.57, dan 11.59 menjadi
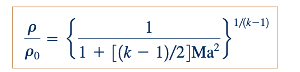
Hubungan ini digambarkan di pinggir untuk udara.
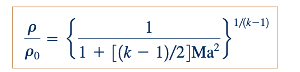

Salah satu cara yang sangat berguna untuk melacak keadaan aliran isentropik dari gas ideal melibatkan diagram suhu–entropi (T–s), seperti yang ditunjukkan dalam Gambar 11.7. Pengalaman telah menunjukkan bahwa garis-garis tekanan konstan umumnya seperti yang digambarkan dalam Gambar 11.7. Aliran isentropik terbatas pada garis vertikal pada diagram T–s. Garis vertikal dalam Gambar 11.7 mewakili aliran antara keadaan stagnasi dan setiap keadaan di dalam nosel konvergen–divergen. Persamaan 11.56 menunjukkan bahwa suhu fluida menurun dengan peningkatan nomor Mach. Dengan demikian, tingkat suhu yang lebih rendah pada diagram T–s sesuai dengan nomor Mach yang lebih tinggi. Persamaan 11.59 menyarankan bahwa tekanan fluida juga menurun dengan peningkatan nomor Mach. Dengan demikian, suhu dan tekanan fluida yang lebih rendah terkait dengan nomor Mach yang lebih tinggi dalam contoh nosel konvergen–divergen isentropik kita.
Salah satu cara untuk menghasilkan aliran melalui nosel konvergen–divergen seperti yang ada di Gambar 11.6a adalah dengan menghubungkan ujung hulu nosel ke pompa vakum. Ketika tekanan di ujung hilir nosel (tekanan belakang) sedikit berkurang, udara akan mengalir dari atmosfer melalui nosel dan pompa vakum. Dengan mengabaikan gesekan dan transfer panas serta mempertimbangkan udara sebagai gas ideal, Persamaan 11.56, 11.59, dan 11.60 serta diagram T–s dapat digunakan untuk menjelaskan aliran stabil melalui nosel konvergen–divergen.
Jika tekanan di dalam saluran hanya sedikit lebih rendah dari tekanan atmosfer, kita memprediksi dengan Persamaan 11.59 bahwa tingkat nomor Mach di dalam saluran akan rendah. Dengan demikian, dengan Persamaan 11.60 kita menyimpulkan bahwa variasi kerapatan fluida di dalam saluran juga kecil. Persamaan kontinuitas (Persamaan 11.402) membawa kita untuk menyatakan bahwa ada sedikit percepatan aliran fluida di bagian konvergen saluran diikuti oleh perlambatan aliran di bagian divergen saluran. Kita telah mempertimbangkan jenis aliran ini ketika kita membahas pengukur Venturi di Bagian 3.6.3. Diagram T – s untuk aliran ini digambarkan dalam Gambar 11.8.
Selanjutnya, kita pertimbangkan apa yang terjadi ketika tekanan belakang diturunkan lebih jauh. Karena aliran dimulai dari diam di hulu bagian konvergen saluran dari Gambar 11.6a, Persamaan 11.48 dan 11.50 mengungkapkan kepada kita bahwa aliran hingga tenggorokan nosel dapat dipercepat hingga mencapai nomor Mach maksimum yang diizinkan 1 di tenggorokan. Dengan demikian, ketika tekanan belakang saluran diturunkan cukup, nomor Mach di tenggorokan saluran akan menjadi 1. Penurunan tekanan belakang lebih lanjut tidak akan mempengaruhi aliran di bagian konvergen saluran karena, seperti yang dibahas di Bagian 11.3, informasi tentang tekanan tidak dapat bergerak ke hulu ketika Ma = 1. Ketika Ma = 1 di tenggorokan nosel konvergen–divergen, kita memiliki kondisi yang disebut aliran tersumbat. Beberapa persamaan berguna untuk aliran tersumbat dikembangkan di bawah ini.
Kita sudah menggunakan kondisi stagnasi untuk yang Ma = 0 sebagai kondisi referensi. Akan berguna bagi kita untuk menggunakan kondisi yang terkait dengan Ma = 1 dan tingkat entropi yang sama dengan fluida yang mengalir sebagai kondisi referensi lain yang akan kita sebut sebagai kondisi kritis, dilambangkan sebagai ( )*.
Rasio tekanan di tenggorokan saluran konvergen–divergen untuk aliran tersumbat, p, terhadap tekanan stagnasi, p0, disebut sebagai rasio tekanan kritis. Dengan mensubstitusikan Ma = 1 ke dalam Persamaan 11.59, kita mendapatkan
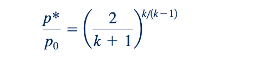


Untuk k=1.4, nilai nominal k untuk udara, Persamaan 11.61 menghasilkan
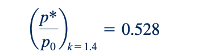
Karena tekanan stagnasi untuk contoh saluran konvergen-diverjen kita adalah tekanan atmosfer, p atm , maka tekanan tenggorokan untuk aliran udara yang tercekik adalah, dari Persamaan 11.62
Kita dapat mendapatkan hubungan untuk rasio suhu kritis, T*/T0 , dengan mensubstitusikan Ma=1 ke dalam Persamaan 11.56. Dengan demikian,
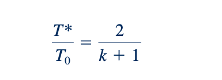
atau untuk k=1.4,
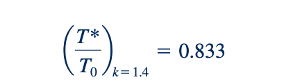
Untuk saluran pada Gambar 11.6a, Persamaan 11.64 memberikan

Tekanan stagnasi dan kritis serta suhu ditunjukkan pada diagram T–s pada Gambar 11.9.
Ketika kita menggabungkan persamaan gas ideal (Eq. 11.12) dengan Persamaan 11.61 dan 11.63, untuk Ma = 1 kita mendapatkan

Untuk udara (k = 1.42), Persamaan 11.65 menghasilkan:
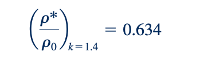
dan kita melihat bahwa ketika aliran pipa konvergen-divergen tercekik, kerapatan udara di tenggorokan pipa adalah 63,4% dari kerapatan udara atmosfer.



Aliran isentropik Eqs. 11.56, 11.59, dan 11.60 telah digunakan untuk membangun Gambar D.1 di Lampiran D untuk udara (k = 1.42). Contoh 11.6 dan 11.7 mengilustrasikan bagaimana grafik-grafik T/T0, p/p0, dan 𝜌/𝜌0 sebagai fungsi dari Nomor Mach, Ma, dapat digunakan untuk menyelesaikan masalah aliran kompresibel.



Juga termasuk dalam Gambar D.1 adalah grafik rasio luas lokal, A, terhadap luas kritis, A*, untuk nilai-nilai yang berbeda dari Nomor Mach lokal. Pentingnya rasio area ini dijelaskan di bawah ini.
Untuk aliran yang tercekik melalui saluran berkonvergensi-mengkonvergensi dari Gambar 11.6a, persamaan pelestarian massa (Eq. 11.40) menghasilkan

Atau

Dari Eqs. 11.36 dan 11.46, kita dapatkan

Dan

Dengan menggabungkan Eqs. 11.67, 11.68, dan 11.69, kita mendapatkan
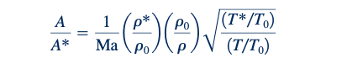
Penyatuan dari Eqs. 11.56, 11.60, 11.63, 11.65, dan 11.70 menghasilkan
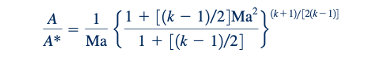
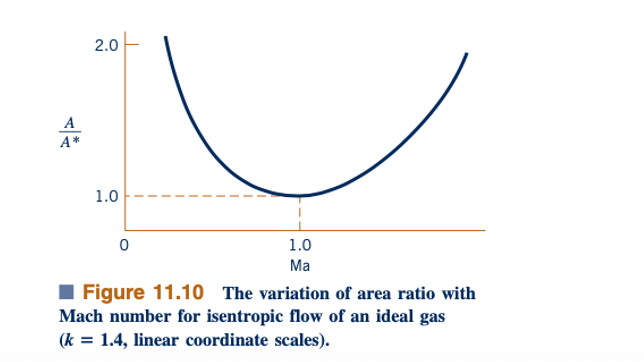
Persamaan 11.71 digunakan untuk menghasilkan nilai-nilai A/A* untuk udara (k = 1.42) dalam Fig. D.1. Nilai-nilai A/A* ini dipetakan sebagai fungsi dari nomor Mach dalam Fig. 11.10. Seperti yang ditunjukkan dalam contoh-contoh berikut, apakah area kritis, A*, secara fisik hadir dalam aliran atau tidak, rasio area, A/A*, tetap merupakan konsep yang berguna untuk aliran isentropik dari gas ideal melalui saluran menyempit dan melebar.
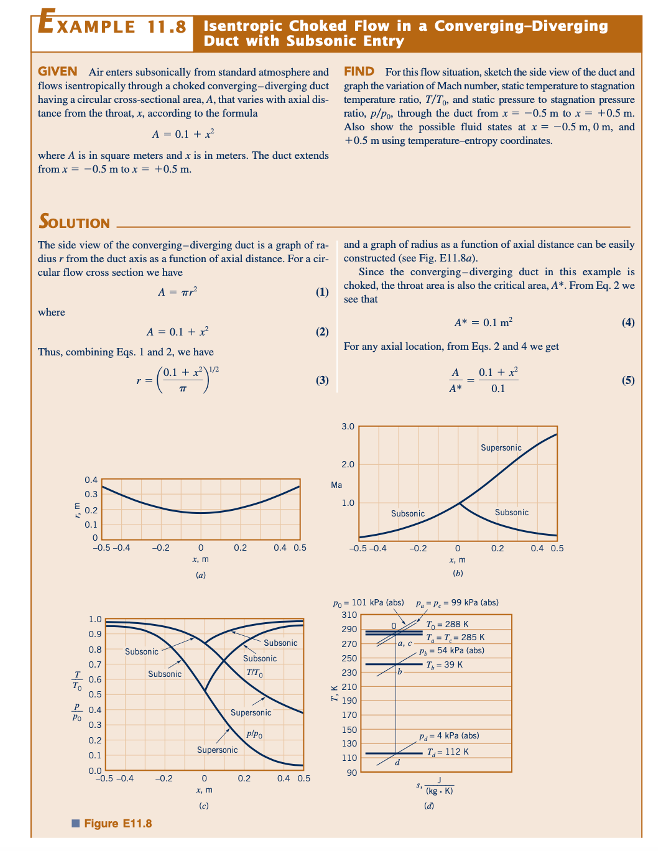
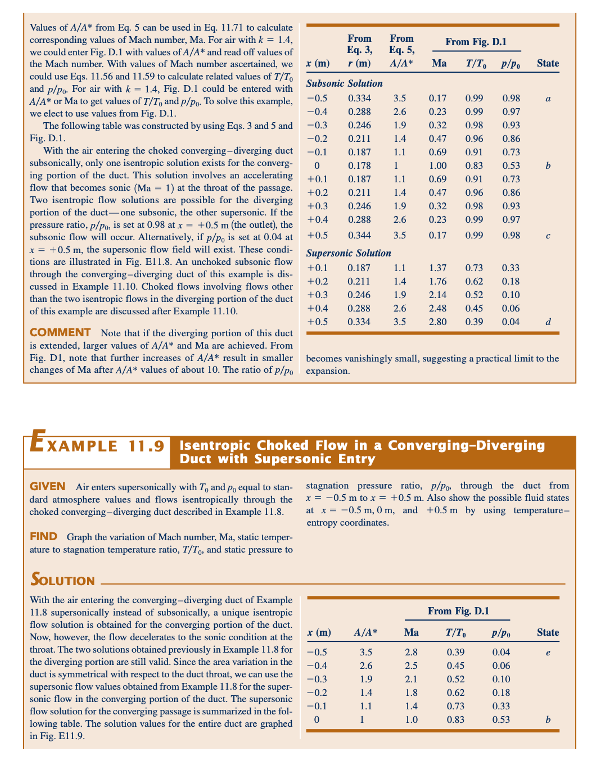
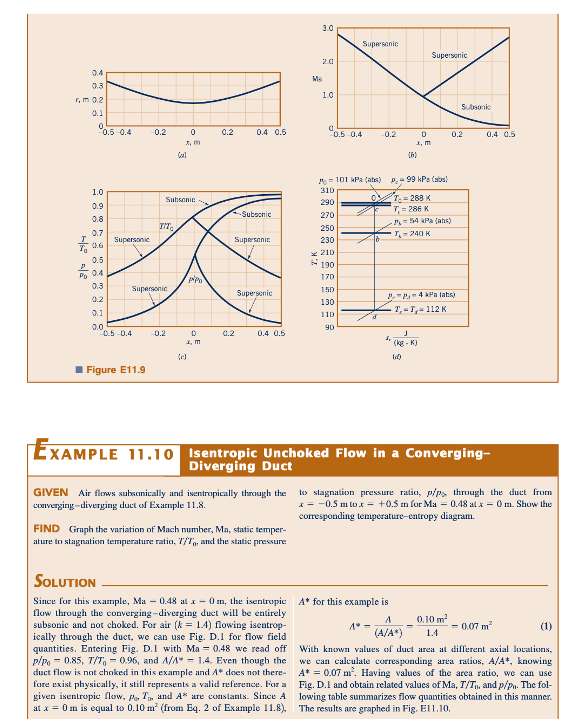
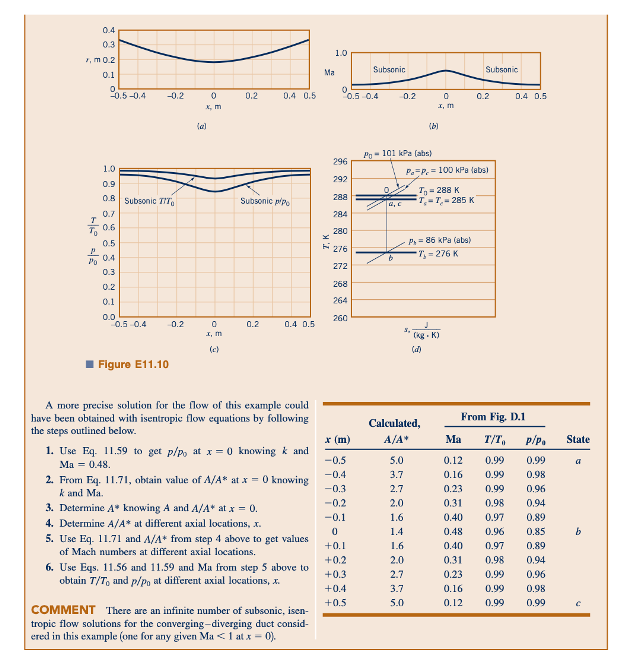
Perilaku aliran isentropik untuk saluran menyempit dan melebar yang dibahas dalam Contoh 11.8, 11.9, dan 11.10 dirangkum dalam grafik rasio area-nomor Mach yang digambarkan dalam Fig. 11.11. Titik a, b, dan c mewakili keadaan pada jarak aksial x ≥ 0,5 m, 0 m, dan ≤ -0,5 m. Pada Fig. 11.11a, aliran isentropik melalui saluran menyempit dan melebar adalah Subsonic tanpa sumbatan di tenggorokan. Situasi ini dibahas dalam Contoh 11.10. Figur 11.11b mewakili aliran sumbatan Subsonic ke Subsonic (Contoh 11.82), dan Figur 11.11c adalah untuk aliran sumbatan Subsonic ke Supersonic (juga Contoh 11.82). Keadaan dalam Fig. 11.11d terkait dengan aliran sumbatan Supersonic ke Supersonic dari Contoh 11.9; keadaan dalam Fig. 11.11e adalah untuk aliran sumbatan Supersonic ke Subsonic dari Contoh 11.9. Tidak dicakup oleh contoh tetapi juga mungkin adalah keadaan aliran isentropik a, b, dan c yang ditunjukkan dalam Fig. 11.11f untuk aliran Supersonic ke Supersonic tanpa sumbatan. Enam kategori ini umumnya mewakili jenis aliran gas ideal isentropik yang mungkin melalui saluran menyempit dan melebar.
Untuk suatu kondisi stagnasi tertentu (yaitu, suhu dan tekanan tetap), gas ideal dengan nilai k konstan, dan geometri saluran menyempit dan melebar, terdapat jumlah solusi aliran isentropik tak berhingga dari Subsonic ke Subsonic (tanpa sumbatan) dan dari Supersonic ke Supersonic (tanpa sumbatan). Sebaliknya, solusi aliran isentropik dari Subsonic ke Supersonic (sumbatan), Subsonic ke Subsonic (sumbatan), Supersonic ke Subsonic (sumbatan), dan Supersonic ke Supersonic (sumbatan) masing-masing bersifat unik. Solusi aliran isentropik yang disebutkan di atas

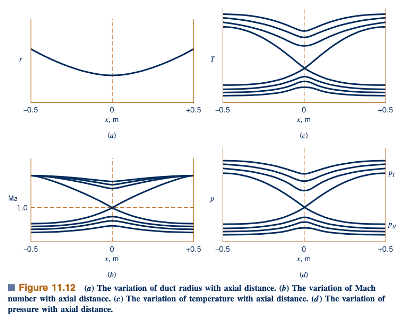
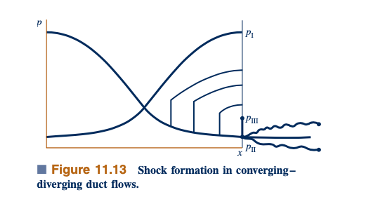
Solusi aliran yang terpresentasikan dalam Gambar 11.12. Ketika tekanan di x = -0,5 (pintu keluar) lebih besar atau sama dengan pI seperti yang ditunjukkan pada Gambar 11.12d, aliran isentropik dimungkinkan. Ketika tekanan di x = -0,5 sama dengan atau kurang dari pII, aliran isentropik dalam saluran dimungkinkan. Namun, ketika tekanan keluar lebih kecil dari pI dan lebih besar dari pIII seperti yang ditunjukkan pada Gambar 11.13, aliran isentropik tidak lagi dimungkinkan dalam saluran. Penentuan nilai pIII dibahas dalam Contoh 11.19.
Beberapa aliran tercekik non-isentropik yang mungkin melalui saluran berkonvergensi-divergensi kita direpresentasikan dalam Gambar 11.13. Setiap kenaikan tekanan tiba-tiba yang ditunjukkan di dalam dan di pintu keluar aliran terjadi melintasi diskontinuitas aliran yang sangat tipis yang disebut gelombang kejut normal. Kecuali untuk aliran melintasi gelombang kejut normal, aliran tersebut isentropik. Persamaan aliran non-isentropik yang menggambarkan perubahan properti fluida yang terjadi melintasi gelombang kejut normal dikembangkan dalam Bagian 11.5.3. Kenaikan atau penurunan tekanan yang kurang tiba-tiba setelah aliran meninggalkan saluran adalah non-isentropik dan dapat diatribusikan pada gelombang kejut oblik tiga dimensi atau gelombang ekspansi. Jika tekanan naik setelah keluar dari saluran, aliran dianggap terlalu diperluas. Jika tekanan turun setelah keluar dari saluran, aliran disebut kurang diperluas. Detail lebih lanjut tentang aliran terlalu diperluas dan kurang diperluas serta gelombang kejut oblik berada di luar cakupan teks ini. Pembaca yang tertarik dapat merujuk ke