Aliran Saluran Luas Konstan Adiabatik dengan Gesekan (Fanno Mengalir)
Aliran saluran luas konstan adiabatik dengan gesekan (Fanno mengalir). Pertimbangkan aliran gas ideal yang stabil, satu dimensi, dan adiabatik melalui saluran dengan area konstan seperti yang ditunjukkan pada Gambar 11.15. Ini adalah aliran Fanno. Untuk volume kontrol yang ditunjukkan, persamaan energi (Persamaan 5.69) mengarah kepada


Atau

di mana ℎ0 adalah entalpi stagnasi. Untuk gas ideal, dari Persamaan 11.9, kita dapat menyimpulkan
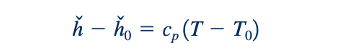
sehingga dengan menggabungkan Persamaan 11.72 dan 11.73, kita mendapatkan
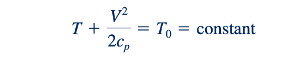
Atau

Dengan mensubstitusikan persamaan keadaan gas ideal (Eq. 11.12) ke dalam Persamaan 11.74, kita mendapatkan

Dari persamaan kontinuitas (Eq. 11.402), kita dapat menyimpulkan bahwa hasil perkalian antara kerapatan dan kecepatan fluida, pV, konstan untuk aliran Fanno tertentu karena luas, A, konstan. Selain itu, untuk aliran Fanno tertentu, suhu stagnasi, T0, tetap. Oleh karena itu, Persamaan 11.75 memungkinkan kita untuk menghitung nilai suhu fluida yang sesuai dengan nilai tekanan fluida dalam aliran Fanno. Kita tunda pembahasan tentang bagaimana tekanan ditentukan hingga nanti.
Seperti diskusi sebelumnya dalam bab ini, berguna untuk menggambarkan aliran Fanno dengan diagram suhu–entropi. Dari persamaan kedua T ds, suatu ekspresi untuk variasi entropi telah diperoleh sebelumnya (Eq. 11.222). Jika suhu, T1, tekanan, p1, dan entropi, s1, di pintu masuk saluran aliran Fanno dianggap sebagai nilai referensi, maka Eq. 11.22 menghasilkan
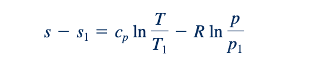
Persamaan 11.75 dan 11.76 bersama-sama menghasilkan kurva dengan koordinat T–s seperti yang diilustrasikan dalam Gambar 11.16. Kurva ini melibatkan gas tertentu (dengan nilai cp dan R tertentu) dengan nilai tetap suhu stagnasi, hasil perkalian kerapatan–kecepatan, dan suhu, tekanan, dan entropi masuk. Kurva seperti yang digambarkan dalam Gambar 11.16 disebut sebagai garis Fanno.



Kita dapat mempelajari lebih lanjut tentang garis Fanno dengan menganalisis lebih lanjut persamaan yang menggambarkan fisika yang terlibat. Sebagai contoh, persamaan kedua T ds (Eq. 11.182) adalah:

Untuk sebuah gas ideal

Dan
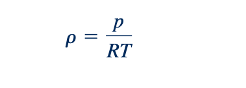
Atau
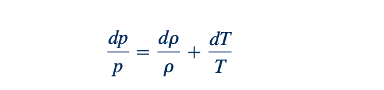
Jadi, dengan menggabungkan Persamaan 11.1, 11.7, 11.18, dan 11.77, kita mendapatkan

Juga, dari persamaan kontinuitas (Eq. 11.402), kita dapatkan untuk aliran Fanno ρV konstan, atau

Menggantikan Persamaan 11.79 ke Persamaan 11.78 menghasilkan

Atau

Dengan melakukan diferensiasi pada persamaan energi 11.742 yang diperoleh sebelumnya, kita mendapatkan


yang, saat disubstitusi ke dalam Persamaan 11.80, menghasilkan

Pada titik tersebut, kita dapat menyimpulkan bahwa perubahan dalam entropi adalah nol.
Persamaan 11.83 menyiratkan bahwa dalam titik a, di mana ds/dT =0, perubahan dalam entropi dengan perubahan dalam suhu adalah nol.

Pada titik a, Mach number adalah 1. Karena suhu stagnasi sama untuk semua titik pada garis Fanno [lihat persamaan energi 1Persamaan 11.742], suhu pada titik a adalah suhu kritis, T* , untuk seluruh garis Fanno. Dengan demikian, aliran Fanno yang sesuai dengan bagian dari garis Fanno di atas suhu kritis harus bersubsonik, dan aliran Fanno pada garis di bawah T* harus bersupersonik.
Hukum kedua termodinamika menyatakan bahwa, berdasarkan semua pengalaman masa lalu, entropi hanya dapat tetap konstan atau meningkat untuk aliran adiabatik. Agar aliran Fanno konsisten dengan hukum kedua termodinamika, aliran hanya dapat berlanjut sepanjang garis Fanno menuju ke titik a, yaitu keadaan kritis. Keadaan kritis mungkin atau mungkin tidak tercapai oleh aliran. Jika tercapai, aliran Fanno tercekik. Beberapa contoh perilaku aliran Fanno disajikan dalam Gambar 11.17. Kasus yang melibatkan aliran Fanno bersubsonik yang dipercepat oleh gesekan hingga mencapai Mach number yang lebih tinggi tanpa tercekik diilustrasikan dalam Gambar 11.17a. Aliran supersonik yang diperlambat oleh gesekan hingga mencapai Mach number yang lebih rendah tanpa tercekik diilustrasikan dalam Gambar 11.17b. Dalam Gambar 11.17c, perubahan tiba-tiba dari aliran supersonik menjadi subsonik dalam saluran Fanno diwakili. Perlambatan mendadak ini terjadi melintasi gelombang kejut normal yang berdiri yang dijelaskan secara lebih detail di Bagian 11.5.3.
Aspek kualitatif dari aliran Fanno yang telah kita diskusikan disarikan dalam Tabel 11.1 dan Gambar 11.18. Untuk memperkirakan perilaku aliran Fanno secara kuantitatif, kita perlu menggabungkan hubungan yang mewakili hukum momentum linear dengan kumpulan persamaan yang sudah kita turunkan dalam bab ini.
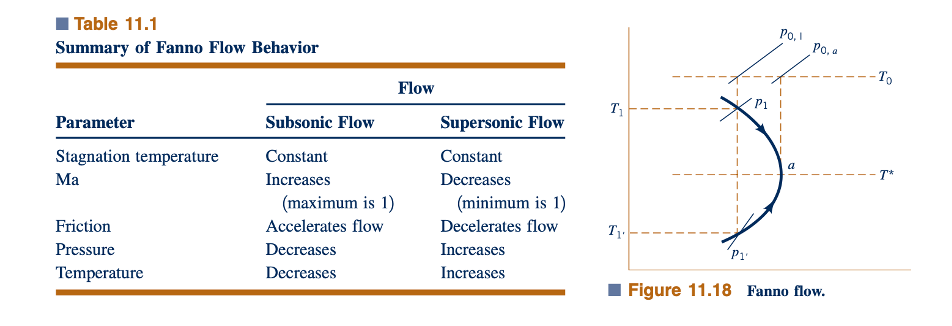
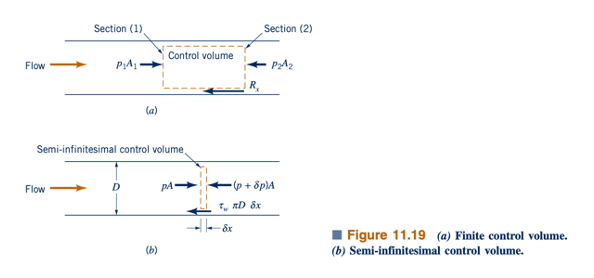
Jika persamaan momentum linear (Persamaan 5.22) diterapkan pada aliran Fanno melalui volume kontrol yang digambarkan pada Gambar 11.19a, hasilnya adalah

dimana R adalah gaya gesek yang diberikan oleh dinding pipa dalam pada fluida. Karena A1=A2=A dan m⋅pAV=konstan (yaitu pV=p1V1=p2V2), kita dapatkan

Bentuk diferensial dari Persamaan 11.84, yang berlaku untuk aliran Fanno melalui volume kontrol semi-infinitesimal seperti yang ditunjukkan dalam Gambar 11.19b, adalah:
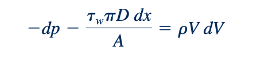
Tegangan geser dinding, τw , berhubungan dengan faktor gesekan dinding, f, dengan Persamaan 8.20 sebagai:

Dengan mensubstitusikan Persamaan 11.86 dan A= 𝜋D2/4 ke dalam Persamaan 11.85, kita mendapatkan:
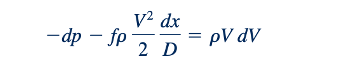
Atau
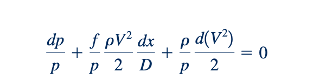
Dengan menggabungkan persamaan keadaan gas ideal (Persamaan 11.12), persamaan kecepatan suara gas ideal (Persamaan 11.36), dan definisi bilangan Mach (Persamaan 11.46) dengan Persamaan 11.88, kita dapatkan:
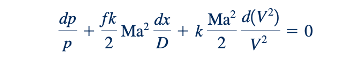
Karena V=Ma c dan c= √(𝑅𝑇𝑘 , maka
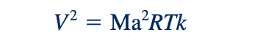
Atau
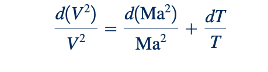
Jika persamaan energi (5.692) diterapkan pada aliran Fanno menghasilkan persamaan (11.74). Jika (11.74) didiferensialkan dan dibagi dengan suhu, maka hasilnya adalah

Substitusi Ekuasi 11.14, 11.36, dan 11.46 ke dalam Persamaan 11.91 menghasilkan

yang dapat digabungkan dengan Persamaan 11.90 untuk membentuk

Kita dapat menggabungkan Persamaan 11.77, 11.79, dan 11.90 menjadi:

Mengkonsolidasikan Persamaan 11.94 dan 11.89 menghasilkan:
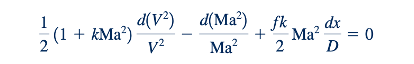
Terakhir, dengan menggabungkan Persamaan 11.93 ke dalam Persamaan 11.95, kita dapat memperoleh:
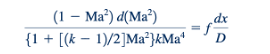
Persamaan 11.96 11.96 dapat diintegrasikan dari satu bagian ke bagian lain dalam saluran aliran Fanno. Kami memilih untuk menggunakan keadaan kritis (*) sebagai referensi dan mengintegrasikan Persamaan 11.96 dari suatu keadaan hulu ke keadaan kritis. Oleh karena itu, kita dapat menulis:

di mana ℓ adalah panjang yang diukur dari suatu lokasi referensi hulu yang sewenang-wenang tetapi tetap ke sebuah bagian dalam aliran Fanno. Untuk solusi perkiraan, kita dapat mengasumsikan bahwa faktor gesekan konstan pada nilai rata-rata selama panjang integrasi, ℓ* -ℓ. Kita juga mempertimbangkan nilai tetap dari k. Dengan demikian, kita dapat memperoleh dari Persamaan 11.97 bahwa:
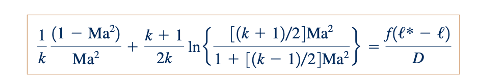

Untuk suatu gas tertentu, nilai-nilai f(ℓ* - ℓ)/D dapat dijadwalkan dalam bentuk tabel sebagai fungsi dari angka Mach untuk aliran Fanno. Sebagai contoh, nilai-nilai f(ℓ* - ℓ )/D untuk aliran Fanno udara dengan (k=1.4) dapat digambarkan sebagai fungsi dari angka Mach dalam Figur D.2 di Lampiran D dan dalam gambar di pinggiran halaman. Perlu diperhatikan bahwa keadaan kritis tidak harus ada dalam aliran Fanno yang sebenarnya sedang dipertimbangkan, karena untuk dua bagian mana pun dalam suatu aliran Fanno yang diberikan, persamaan energi 1Eq. 11.96 menyatakan bahwa penurunan panjang pipa karena gesekan akan menjadi nol ketika Mach number mencapai 1.

Garis besar dalam Gambar 11.20 mengilustrasikan makna fisik dari Persamaan 11.99.
Untuk suatu aliran Fanno tertentu (rasio panas spesifik konstan, diameter saluran, dan faktor gesekan), panjang saluran yang diperlukan untuk mengubah angka Mach dari Ma 1 menjadi Ma 2 dapat ditentukan dari Persamaan 11.98 dan 11.99 atau grafik seperti Figur D.2. Untuk mendapatkan nilai-nilai sifat-sifat fluida lainnya dalam medan aliran Fanno, kita perlu mengembangkan lebih banyak persamaan.

Dengan menggabungkan Persamaan 11.90 dan 11.92, kita dapatkan
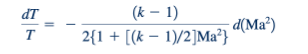
Mengintegrasikan Persamaan 11.100 dari setiap keadaan hulu dalam aliran Fanno ke keadaan kritis (*) menghasilkan
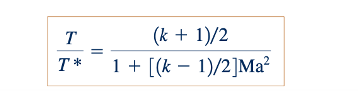

Persamaan 11.68 dan 11.69 memungkinkan kita untuk menuliskan
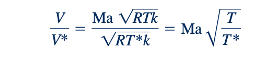
Menggantikan Persamaan 11.101 ke dalam Persamaan 11.102 menghasilkan
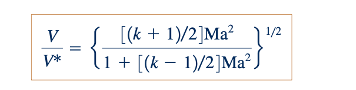

Persamaan 11.101 dan 11.103 digambarkan di pinggir halaman untuk udara.
Dari persamaan kontinuitas (Eq. 11.402) kita dapatkan untuk aliran Fanno.

Gabungan antara 11.104 dan 11.103 menghasilkan:
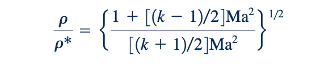
Penerapan persamaan keadaan gas ideal (Eq. 11.12) menghasilkan:

dan menggabungkan Eqs. 11.106, 11.105, dan 11.101 memberikan:


Hubungan ini digambarkan di pinggir untuk udara. Akhirnya, rasio tekanan stagnasi dapat ditulis sebagai:

yang dengan menggunakan Persamaan 11.59 dan 11.107 menghasilkan:

Nilai-nilai f (ℓ* - ℓ)/D, T/T*, V/V*, p/p*, dan p0/p*0 untuk aliran Fanno udara dengan (k=1.4) ditampilkan sebagai fungsi dari jumlah Mach (menggunakan Persamaan 11.99, 11.101, 11.103, 11.107, dan 11.109) dalam Fig. D.2 di Lampiran D. Kegunaan Fig. D.2 diilustrasikan dalam Contoh 11.12, 11.13, dan 11.14. Lihat Ref. 7 untuk materi aliran internal yang lebih kompresibel.




