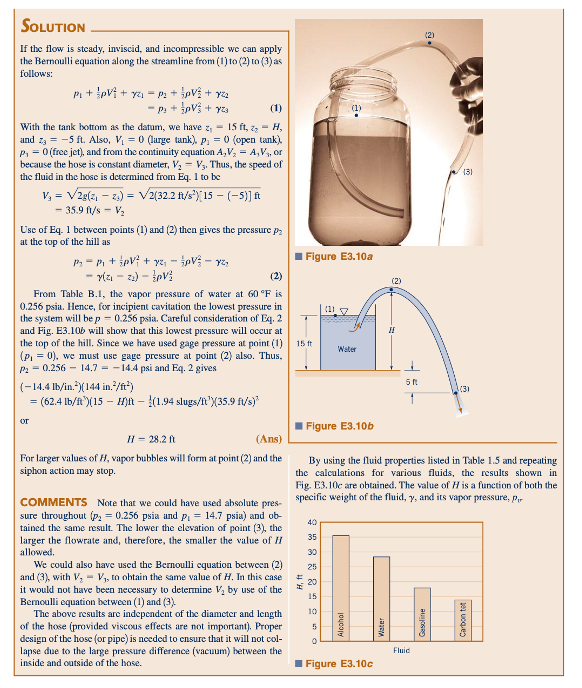
Arus Terbatas
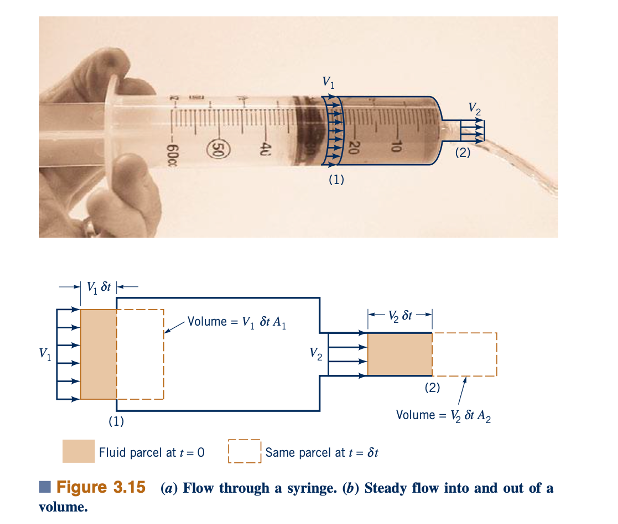
Arus terbatas. Dalam banyak kasus, fluida dibatasi secara fisik dalam suatu perangkat sehingga tekanannya tidak dapat ditentukan sebelumnya seperti yang dilakukan dalam contoh jet bebas di atas. Kasus-kasus tersebut termasuk nozzle dan pipa berdiameter variabel di mana kecepatan fluida berubah karena luas aliran berbeda dari satu bagian ke bagian lainnya. Untuk situasi seperti ini, perlu menggunakan konsep pelestarian massa (persamaan kontinuitas) bersama dengan persamaan Bernoulli. Turunan dan penggunaan persamaan ini dibahas secara detail dalam Bab 4 dan 5. Untuk keperluan bab ini, kita dapat menggunakan bentuk yang disederhanakan dari persamaan kontinuitas yang diperoleh dari argumen intuitif berikut. Pertimbangkan fluida yang mengalir melalui volume tetap (seperti sebuah suntikan) yang memiliki satu saluran masuk dan satu saluran keluar seperti yang ditunjukkan dalam Gambar 3.15a. Jika aliran tersebut tetap sehingga tidak ada penambahan cairan tambahan dalam volume tersebut, laju aliran fluida ke dalam volume harus sama dengan laju aliran keluar dari volume tersebut (jika tidak, massa tidak akan terjaga).
Laju aliran massa dari sebuah lubang keluar, m (dalam slug/s atau kg/s), diberikan oleh m =ρQ, di mana Q (dalam ft3/s atau m3/s) adalah laju aliran volume. Jika luas outlet adalah A dan fluida mengalir melintasi area ini (sejajar dengan luas), maka:dengan kecepatan rata-rata V, maka volume fluida yang melintasi area ini dalam selang waktu 𝛿t adalah VA 𝛿t, sama dengan volume dalam sebuah ruang berpanjang V 𝛿t dan berpenampang A (lihat Gambar 3.15b). Oleh karena itu, laju aliran volume (volume per unit waktu) adalah Q = VA. Dengan demikian, massa m = ρVA. Untuk memelihara massa, laju aliran masuk harus sama dengan laju aliran keluar. Jika masukannya ditentukan sebagai (1)dan keluarnya sebagai (2), maka m1= m2. Dengan demikian, pelestarian massa mengharuskan
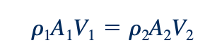
Jika densitas tetap konstan, maka ρ1=ρ2, dan persamaan di atas menjadi persamaan kontinuitas untuk aliran tak dapat dipadatkan.
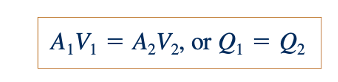
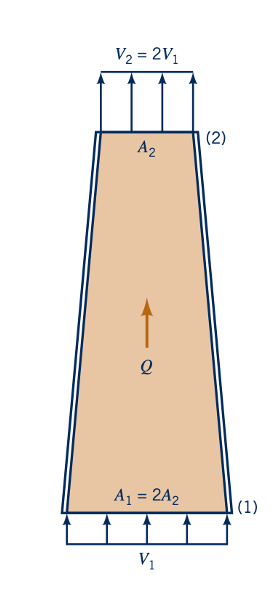
Misalnya, jika seperti yang ditunjukkan oleh gambar di sisi, luas aliran outlet adalah separuh dari luas aliran inlet, maka kecepatan outlet adalah dua kali kecepatan inlet, karena
V1 = A1 V1/A2 = 2 V1. Penggunaan persamaan Bernoulli dan persamaan laju aliran 1persamaan kontinuitas2 ditunjukkan dalam Contoh 3.7.
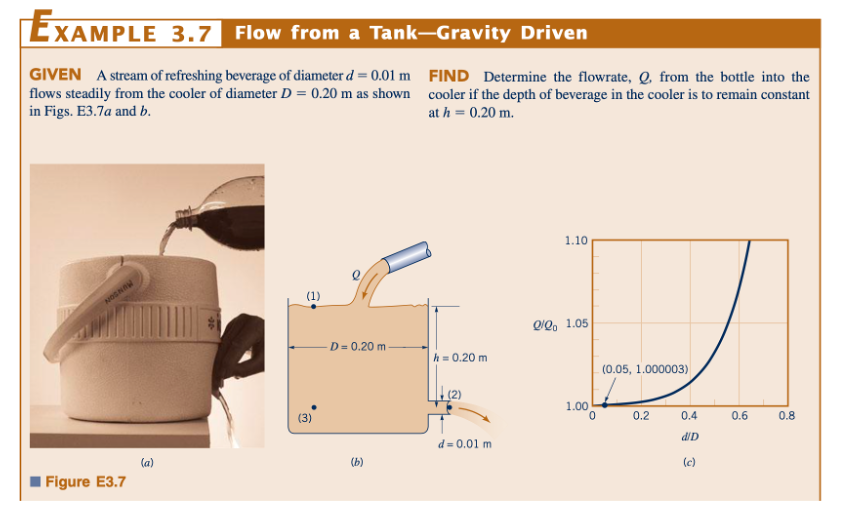

Fakta bahwa perubahan energi kinetik seringkali disertai dengan perubahan tekanan ditunjukkan oleh Contoh 3.8.

Dalam banyak situasi, efek gabungan energi kinetik, tekanan, dan gravitasi penting. Contoh 3.9 mengilustrasikannya.

Secara umum, peningkatan kecepatan disertai dengan penurunan tekanan. Sebagai contoh, kecepatan udara yang mengalir di atas permukaan sayap pesawat terbang, secara rata-rata, lebih cepat daripada yang mengalir di bawah permukaan bagian bawah. Oleh karena itu, gaya tekanan bersih lebih besar di bagian bawah daripada di bagian atas—sayap menghasilkan gaya angkat.
Jika perbedaan kecepatan cukup besar, perbedaan tekanan juga bisa signifikan. Untuk aliran gas, hal ini dapat memperkenalkan efek kompresibilitas seperti yang dibahas di Bagian 3.8 dan Bab 11. Untuk aliran cairan, ini dapat mengakibatkan kavitasi, situasi berbahaya yang terjadi ketika tekanan cairan turun menjadi tekanan uap dan cairan "mendidih".
Seperti yang dibahas dalam Bab 1, tekanan uap, pv , adalah tekanan di mana gelembung uap terbentuk dalam cairan. Ini adalah tekanan di mana cairan mulai mendidih. Jelas bahwa tekanan ini bergantung pada jenis cairan dan suhunya. Sebagai contoh, air, yang mendidih pada 212 °C pada tekanan atmosfer standar, 14,7 atm, mendidih pada 80 °C jika tekanannya adalah 0,507 atm. Artinya, pv=0,507 atm pada 80°C dan pv=14,7 atm pada 212 °C.
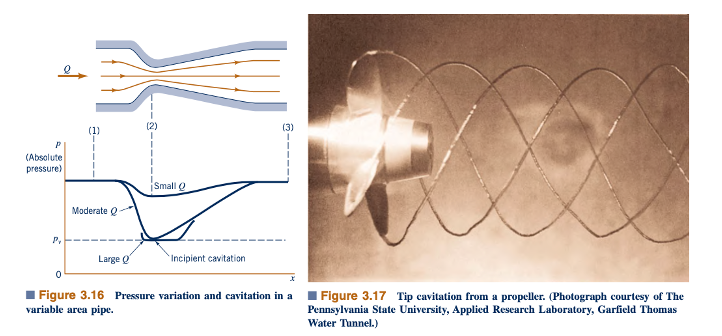
Salah satu cara untuk menghasilkan kavitasi dalam cairan yang mengalir dicatat dari persamaan Bernoulli. Jika kecepatan fluida ditingkatkan (misalnya, dengan mengurangi luas aliran seperti yang ditunjukkan pada Gambar 3.16), tekanan akan menurun. Penurunan tekanan ini (diperlukan untuk mempercepat fluida melalui penyempitan) dapat cukup besar sehingga tekanan dalam cairan berkurang menjadi tekanan uapnya. Contoh sederhana kavitasi dapat ditunjukkan dengan selang kebun biasa. Jika selang tersebut "ditekuk", pembatasan di area aliran seperti yang ditunjukkan pada Gambar 3.16 akan terjadi. Kecepatan air melalui pembatasan ini akan relatif besar. Dengan jumlah pembatasan yang cukup, suara air yang mengalir akan berubah—suara desisan yang pasti terjadi. Suara ini adalah hasil dari kavitasi.
Dalam situasi seperti itu, perebusan terjadi (meskipun suhu tidak perlu tinggi), gelembung uap terbentuk, dan kemudian mereka runtuh saat cairan bergerak ke daerah tekanan yang lebih tinggi (kecepatan yang lebih rendah). Proses ini dapat menghasilkan efek dinamis (implosi) yang menyebabkan perubahan tekanan yang sangat besar di sekitar gelembung. Tekanan sebesar 100.000 psi (690 MPa) diyakini terjadi. Jika gelembung runtuh dekat dengan batas fisik, mereka dapat, dalam jangka waktu tertentu, menyebabkan kerusakan pada permukaan di area kavitasi. Kavitasi ujung dari baling-baling ditunjukkan dalam Gambar 3.17. Dalam kasus ini, rotasi berkecepatan tinggi dari baling-baling menghasilkan tekanan rendah yang sesuai pada baling-baling. Jelas, desain yang tepat dan penggunaan peralatan diperlukan untuk menghindari kerusakan akibat kavitasi.