Aspek Praktis Penggunaan Model
Aspek Praktis Penggunaan Model.
Validasi Desain Model. Sebagian besar studi model melibatkan asumsi vereinfachend yang berkaitan dengan variabel-variabel yang akan dipertimbangkan. Meskipun jumlah asumsi sering kali kurang ketat dibandingkan yang diperlukan untuk model matematika, namun mereka tetap memperkenalkan beberapa ketidakpastian dalam desain model. Oleh karena itu, diinginkan untuk memeriksa desain secara eksperimental bila memungkinkan. Dalam beberapa situasi, tujuan dari model adalah untuk memprediksi efek dari perubahan-perubahan tertentu yang diusulkan dalam suatu prototipe tertentu, dan dalam hal ini beberapa data prototipe aktual mungkin tersedia. Model dapat dirancang, dibangun, dan diuji, dan prediksi model dapat dibandingkan.Dengan data ini. Jika kesepakatan tersebut memuaskan, maka model dapat diubah sesuai dengan keinginan, dan efek yang sesuai pada prototipe dapat diprediksi dengan kepercayaan yang meningkat.
Prosedur lain yang berguna dan informatif adalah melakukan uji coba dengan serangkaian model berbagai ukuran, di mana salah satu model dapat dianggap sebagai prototipe dan yang lainnya sebagai "model" dari prototipe ini. Dengan model-model yang dirancang dan dioperasikan berdasarkan desain yang diusulkan, syarat yang diperlukan untuk validitas desain model adalah bahwa prediksi yang akurat dapat dibuat antara setiap pasang model, karena satu dapat selalu dianggap sebagai model dari yang lain. Meskipun kesepakatan yang sesuai dalam uji validasi seperti ini tidak secara pasti menunjukkan desain model yang benar (misalnya, skala panjang antara model laboratorium mungkin sangat berbeda dari yang diperlukan untuk prediksi prototipe aktual), namun jelas bahwa jika kesepakatan antara model tidak dapat dicapai dalam uji coba ini, tidak ada alasan untuk mengharapkan bahwa desain model yang sama dapat digunakan untuk memprediksi perilaku prototipe secara benar.
Model yang Tidak Sesuai. Meskipun ide umum di balik menetapkan persyaratan kesamaan untuk model cukup sederhana (kita hanya menyamakan pi term), tidak selalu mungkin untuk memenuhi semua persyaratan yang diketahui. Jika satu atau lebih dari persyaratan kesamaan tidak terpenuhi, misalnya, jika Π2m tidak sama dengan Π2, maka akan mengikuti bahwa persamaan prediksi Π1 = Π1m tidak benar; artinya, Π1 tidak sama dengan Π1m. Model-model di mana satu atau lebih persyaratan kesamaan tidak terpenuhi disebut sebagai model yang distorsi.
Model-model yang distorsi cukup umum, dan mereka dapat muncul karena berbagai alasan. Misalnya, mungkin saja cairan yang sesuai tidak dapat ditemukan untuk model. Contoh klasik dari model yang distorsi terjadi dalam studi aliran saluran terbuka atau permukaan bebas. Biasanya, dalam masalah-masalah ini baik jumlah Reynolds, ρVℓ/μ, maupun nomor Froude, V√g/ℓ, terlibat.
Kesamaan nomor Froude memerlukan

Jika model dan prototipe dioperasikan pada medan gravitasi yang sama, maka skala kecepatan yang dibutuhkan adalah
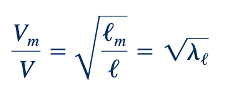
Dibutuhkan kesamaan bilangan Reynolds
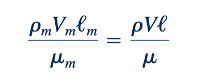
Dan skala kecepatan adalah

karena skala kecepatan harus sama dengan akar kuadrat skala panjang, maka berikut ini