Beberapa Aliran Potensial Bidang Dasar
Beberapa aliran potensial bidang dasar. Karena persamaan Laplace bersifat linear, berbagai solusi dapat ditambahkan untuk mendapatkan solusi lainnya. Artinya, jika ∅1 (x,y,z) dan ∅2 (x,y,z) adalah dua solusi untuk persamaan Laplace, maka ∅3 =∅3+ ∅2 juga merupakan solusi. Sifat ini memungkinkan kita untuk membuat solusi yang lebih rumit dengan menggabungkan solusi-solusi dasar. Pada bagian ini, kita akan mengidentifikasi beberapa potensial kecepatan dasar yang menggambarkan aliran yang relatif sederhana. Potensial dasar ini kemudian akan digabungkan pada bagian berikutnya untuk menggambarkan pola aliran yang lebih kompleks.
Untuk kesederhanaan, kita akan fokus secara eksklusif pada aliran dua dimensi, yang dapat dijelaskan dengan menggunakan koordinat Kartesian.
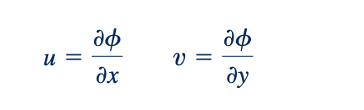
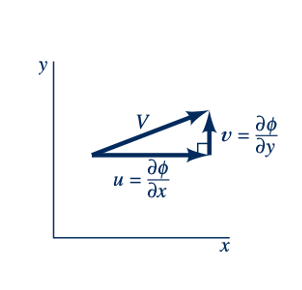
Dengan menggunakan koordinat silindris, persamaan Laplace dapat dituliskan sebagai:
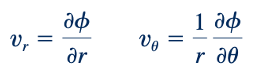
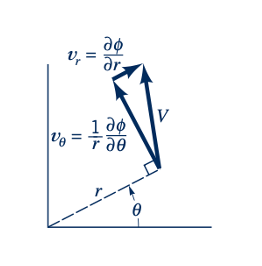
seperti yang ditunjukkan oleh gambar di pinggir. Karena kita dapat mendefinisikan fungsi aliran untuk aliran bidang, kita juga dapat membiarkannya
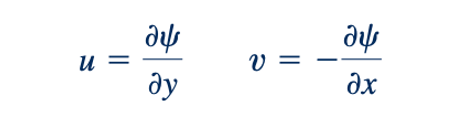
Atau
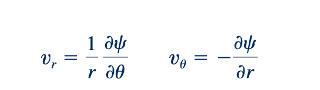
Kita tahu bahwa dengan mendefinisikan kecepatan dalam hal fungsi aliran, kekekalan massa terpenuhi dengan identik. Jika sekarang kita mengimpose kondisi irrotasionalitas, maka dari Persamaan 6.59, ini mengikuti bahwa
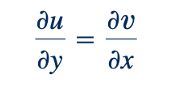
dan dalam hal fungsi aliran
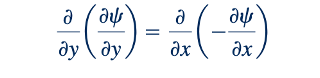
Atau
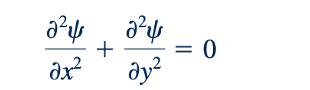
Garis-garis konstan untuk potensial kecepatan adalah garis aliran. Dalam visualisasi aliran, kita dapat membayangkan garis aliran sebagai jalur yang akan diikuti oleh partikel fluida, sedangkan garis-garis ekuipotensial adalah garis di mana kecepatan partikel fluida tetap konstan. Keduanya memberikan wawasan yang berharga tentang perilaku aliran dan merupakan alat analisis yang berguna.
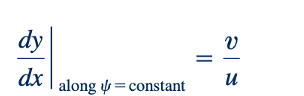
Perubahan ∅ saat kita bergerak dari satu titik (x,y) ke titik terdekat lainnya (x + dx,y+ dy) diberikan oleh hubungan:
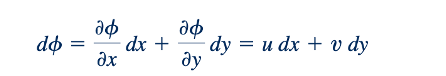
Di sepanjang garis konstan ∅, kita memiliki d∅ = 0, sehingga:
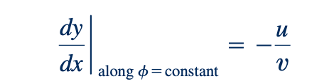
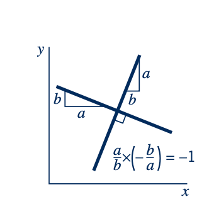
Perbandingan antara Persamaan 6.76 dan 6.77 menunjukkan bahwa garis-garis konstan ∅ (disebut garis-garis equipotensial) tegak lurus terhadap garis-garis konstan 𝜓 (disebut garis arus) di semua titik di mana mereka berpotongan. Untuk setiap medan aliran potensial, sebuah "jaringan aliran" dapat digambar yang terdiri dari sekelompok garis arus dan garis-garis equipotensial. Jaringan aliran berguna untuk memvisualisasikan pola aliran dan dapat digunakan untuk mendapatkan solusi grafis dengan menggambar garis-garis arus dan garis-garis equipotensial, dan menyesuaikan garis-garis tersebut hingga sekitar tegak lurus di semua titik di mana garis-garis tersebut berpotongan. Contoh jaringan aliran ditunjukkan dalam Gambar 6.15. Kecepatan dapat diestimasi dari jaringan aliran, karena kecepatan berbanding terbalik dengan jarak antar garis arus, seperti yang ditunjukkan oleh gambar di sisi. Dengan demikian, misalnya, dari Gambar 6.15, kita dapat melihat bahwa kecepatan di dekat sudut dalam akan lebih tinggi daripada kecepatan di sepanjang bagian luar tikungan. (Lihatlah foto-foto di awal Bab 3 dan 6.)