Bentuk Diferensial Persamaan Kontinuitas
Bentuk diferensial persamaan kontinuitas. Kami akan mengambil elemen kubus kecil dan diam sebagai volume kontrol kami, seperti yang ditunjukkan dalam Gambar 6.5a. Pada pusat elemen, kerapatan fluida adalah ρ, dan kecepatan memiliki komponen u, v, dan w. Karena elemen tersebut kecil, integral volume dalam Persamaan 6.19 dapat diekspresikan sebagai
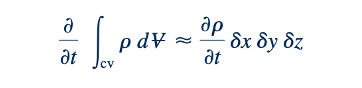

Laju aliran massa melalui permukaan elemen dapat diperoleh dengan mempertimbangkan aliran dalam setiap arah koordinat secara terpisah. Sebagai contoh, dalam Gambar 6.5b aliran dalam arah x digambarkan. Jika kita biarkan ru mewakili komponen x dari laju aliran massa per satuan luas di pusat elemen, maka pada sisi kanan

dan pada sisi kiri
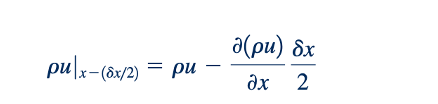
sebagai (𝛿x2), (𝛿x)3, dan seterusnya. Hal ini ditunjukkan oleh gambar di pinggiran. Ketika sisi kanan dari Persamaan 6.21 dan 6.22 dikalikan dengan luas 𝛿y 𝛿z, laju di mana massa melintasi sisi kanan dan kiri elemen diperoleh seperti yang diilustrasikan dalam Gambar 6.5b. Ketika dua ekspresi ini digabungkan, laju bersih massa yang mengalir dari elemen melalui dua permukaan dapat diungkapkan sebagai
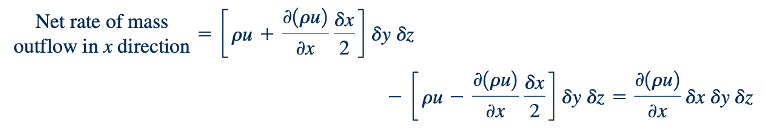

Untuk kesederhanaan, hanya aliran dalam arah x yang dipertimbangkan dalam Gambar 6.5b, tetapi secara umum, akan ada juga aliran dalam arah y dan z. Analisis yang serupa dengan yang digunakan untuk aliran dalam arah x menunjukkan bahwa

Dan
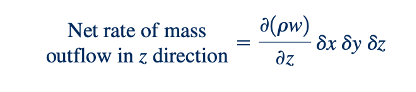
Dengan Demikian
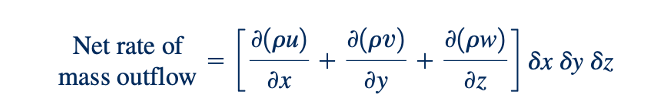
Dari Persamaan 6.19, 6.20, dan 6.26, sekarang dapat disimpulkan bahwa persamaan diferensial untuk konservasi massa adalah
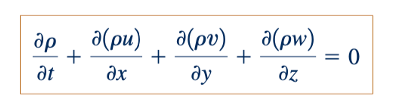
Seperti yang disebutkan sebelumnya, persamaan ini juga sering disebut sebagai persamaan kontinuitas.
Persamaan kontinuitas adalah salah satu persamaan dasar mekanika fluida dan, seperti yang diungkapkan dalam Persamaan 6.27, berlaku untuk aliran yang mantap atau tidak mantap, serta fluida dapat dimampatkan atau tidak dapat dimampatkan. Dalam notasi vektor, Persamaan 6.27 dapat ditulis sebagai
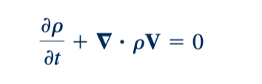
Dua kasus khusus sangat menarik perhatian. Untuk aliran mantap dari fluida dapat dimampatkan
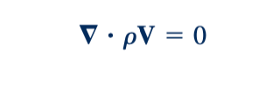
Atau
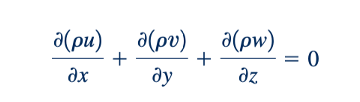
Hal ini mengikuti karena menurut definisi ρ bukanlah fungsi waktu untuk aliran mantap, tetapi bisa menjadi fungsi posisi. Untuk fluida tidak dapat dimampatkan, kerapatan fluida, ρ, adalah konstan di seluruh medan aliran sehingga Persamaan 6.28 menjadi
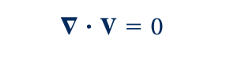
Atau
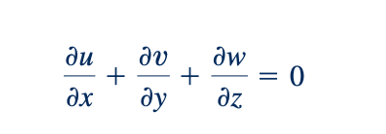
Persamaan 6.31 berlaku baik untuk aliran mantap maupun tidak mantap dari fluida tidak dapat dimampatkan. Perhatikan bahwa Persamaan 6.31 sama dengan yang diperoleh dengan mengatur laju dilatasi volumetrik (Persamaan 6.92) menjadi nol. Hasil ini seharusnya tidak mengejutkan karena kedua hubungan didasarkan pada konservasi massa untuk fluida tidak dapat dimampatkan. Namun, ekspresi untuk laju dilatasi volumetrik dikembangkan dari pendekatan sistem, sedangkan Persamaan 6.31 dikembangkan dari pendekatan volume kontrol. Dalam kasus pertama, deformasi massa fluida diferensial tertentu dipelajari, dan dalam kasus terakhir, aliran massa melalui volume diferensial tetap dipelajari.


