Bilangan Mach dan Kecepatan Suara
Bilangan Mach dan kecepatan suara. Nomor Mach, Ma, diperkenalkan di Bab 1 dan 7 sebagai ukuran tak berdimensi dari pemampatan dalam aliran fluida. Dalam bagian ini dan bagian-bagian berikutnya, kita mengembangkan beberapa hubungan yang berguna yang melibatkan nomor Mach. Nomor Mach didefinisikan sebagai rasio dari nilai kecepatan aliran lokal, V, terhadap kecepatan suara lokal, c. Dengan kata lain,
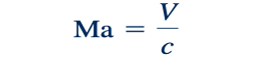
Apa yang kita persepsikan sebagai suara umumnya terdiri dari denyutan tekanan lemah yang bergerak melalui udara dengan Nomor Mach satu. Ketika gendang telinga kita merespons suksesi denyutan tekanan yang bergerak, kita mendengar suara.
Untuk lebih memahami konsep kecepatan suara, kita menganalisis mekanika fluida satu dimensi dari denyutan tekanan yang sangat tipis dan lemah yang bergerak dengan kecepatan suara melalui fluida yang diam (lihat Gambar 11.1a). Di depan denyutan tekanan, kecepatan fluida adalah nol, dan tekanan dan densitas fluida adalah p dan ρ. Di belakang denyutan tekanan, kecepatan fluida telah berubah sebesar 𝛿V, dan tekanan dan densitas fluida juga telah berubah sebesar 𝛿p dan 𝛿ρ. Kita memilih suatu volume kontrol yang sangat tipis yang bergerak bersama dengan denyutan tekanan seperti yang digambarkan.
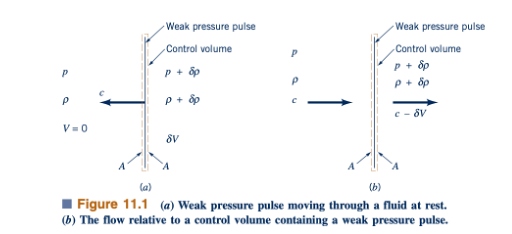
di Gambar 11.1a. Kecepatan denyutan tekanan yang lemah dianggap konstan dan hanya dalam satu arah; oleh karena itu, volume kontrol kita bersifat inersial.
Bagi pengamat yang bergerak dengan volume kontrol ini (Gambar 11.1b), terlihat seolah-olah fluida masuk ke volume kontrol melalui luas permukaan A dengan kecepatan c pada tekanan p dan densitas ρ, dan meninggalkan volume kontrol melalui luas permukaan A dengan kecepatan c−𝛿V, tekanan p−𝛿p, dan densitas ρ−𝛿ρ. Ketika persamaan kontinuitas (Persamaan 5.162) diterapkan pada aliran melalui volume kontrol ini, hasilnya adalah

Atau

Karena (𝛿p) (𝛿V) jauh lebih kecil dari suku lain dalam Persamaan 11.27, kita abaikan dari pertimbangan lebih lanjut dan kita pertahankan
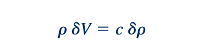
Persamaan momentum linear (Persamaan 5.292) juga dapat diterapkan pada aliran melalui volume kontrol pada Gambar 11.1b. Hasilnya adalah
Perhatikan bahwa gaya-gaya gesek dianggap sangat kecil. Kita sekali lagi mengabaikan suku-suku orde yang lebih tinggi [seperti (𝛿V^2) dibandingkan dengan c 𝛿V, misalnya] dan menggabungkan Persamaan 11.26 dan 11.29 untuk mendapatkan
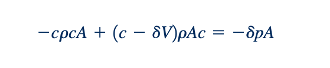
Atau
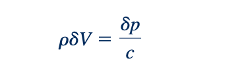
Dari Persamaan 11.28 (kontinuitas) dan 11.30 (momentum linear), kita peroleh
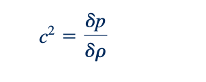
Atau
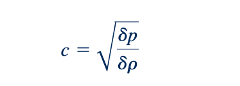
Ekspresi untuk kecepatan suara ini dihasilkan dari penerapan prinsip kekekalan massa dan kekekalan momentum linear pada aliran melalui volume kontrol pada Gambar 11.1b. Prinsip-prinsip ini juga digunakan secara serupa di Bagian 10.2.1 untuk mendapatkan ekspresi untuk kecepatan gelombang permukaan yang bergerak di permukaan fluida dalam sebuah saluran.
Prinsip kekekalan energi juga dapat diterapkan pada aliran melalui volume kontrol pada Gambar 11.1b. Jika persamaan energi (Persamaan 5.1032) digunakan untuk aliran melalui volume kontrol ini, hasilnya adalah
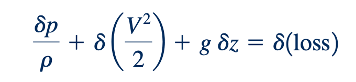
Untuk aliran gas, kita dapat menganggap g𝛿z sebagai sangat kecil dibandingkan dengan suku lain dalam persamaan. Juga, jika kita mengasumsikan bahwa aliran tidak memiliki gesekan, maka 𝛿 (loss)= 0 dan Persamaan 11.32 menjadi
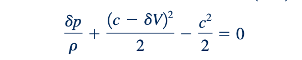
atau, mengabaikan (𝛿V)^2 dibandingkan dengan c 𝛿V, kita dapatkan
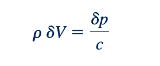
Dengan menggabungkan Persamaan 11.28 (kontinuitas) dan 11.33 (energi), kita sekali lagi mendapati bahwa
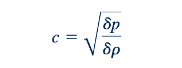
yang identik dengan Persamaan 11.31. Dengan demikian, prinsip kekekalan momentum linear dan prinsip kekekalan energi menghasilkan hasil yang sama. Jika kita juga mengasumsikan bahwa aliran tanpa gesekan melalui volume kontrol pada Gambar 11.1b adalah adiabatik (tanpa transfer panas), maka aliran tersebut adalah isentropik. Pada batasnya, saat 𝛿p menjadi sangat kecil (ketika 𝛿p→𝜕p→0),
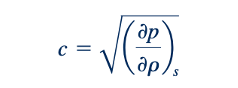
di mana subskrip s digunakan untuk menunjukkan bahwa diferensiasi parsial terjadi pada entropi konstan.
Persamaan 11.34 menyarankan kepada kita bahwa kita dapat menghitung kecepatan suara dengan menentukan turunan parsial tekanan terhadap densitas pada entropi konstan. Untuk aliran isentropik dari gas ideal (dengan cp dan cv konstan), kita telah mempelajari sebelumnya bahwa

Dan dengan demikian
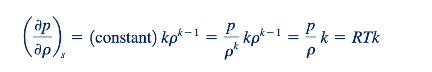
Oleh karena itu, untuk gas ideal

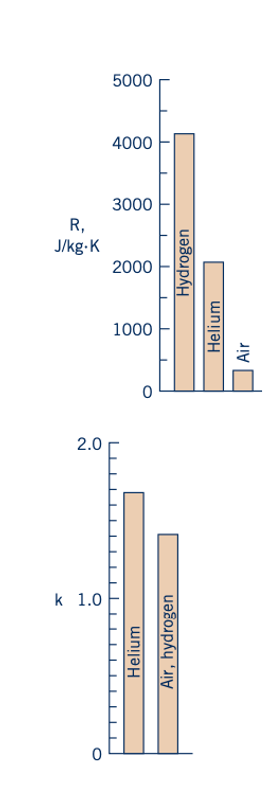
Dari Persamaan 11.36 dan grafik di margin, kita menyimpulkan bahwa untuk suhu tertentu, kecepatan suara, c, dalam hidrogen dan helium lebih tinggi daripada dalam udara.
Secara lebih umum, modulus bulk elastisitas, E, dari setiap fluida termasuk cairan, didefinisikan sebagai
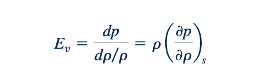
Dengan demikian, secara umum, dari Persamaan 11.34 dan 11.37,
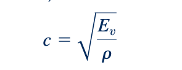
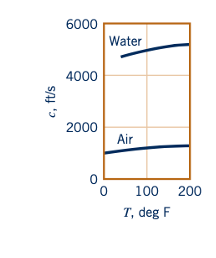
Nilai-nilai kecepatan suara dijelaskan dalam Tabel B.1 dan B.2 untuk air, dan dalam Tabel B.3 dan B.4 untuk udara. Dari pengalaman kita, kita tahu bahwa udara lebih mudah ditekan daripada air. Perhatikan dari nilai-nilai c dalam Tabel B.1 hingga B.4 dan grafik di margin bahwa kecepatan suara dalam udara jauh lebih kecil daripada di air. Dari Persamaan 11.37, kita dapat menyimpulkan bahwa jika suatu fluida benar-benar tak terkompresi, modulus bulknya akan tak terhingga besar, demikian pula dengan kecepatan suara dalam fluida tersebut. Oleh karena itu, aliran tak terkompresibel harus dipertimbangkan sebagai perkiraan yang diidealisis dari realitas.