Perbandingan Berbagai Skema
Perbandingan berbagai skema. Dengan membandingkan stabilitas dari berbagai skema yang telah disajikan sejauh ini, jelas bahwa yang paling negatif (dengan koefisien -3/2) adalah yang terkait dengan skema SOU. Ini diikuti oleh upwind (dengan koefisien -1), kemudian FROMM (dengan koefisien -3/4), setelah itu QUICK (dengan koefisien -3/8), dan akhirnya skema perbedaan pusat (dengan koefisien nol, yaitu sensitivitas netral terhadap perubahan ϕC). Tindakan koreksi diri yang dibahas di atas adalah hasil dari kontribusi baik konveksi maupun difusi. Difusi palsu yang dihasilkan oleh skema upwind menambah stabilitasnya dan meskipun koefisiennya adalah -1, skema ini adalah skema paling stabil. Hal ini ditunjukkan oleh profil yang disajikan dalam Figur 11.14, yang mewakili solusi menggunakan berbagai skema numerik dari persamaan konveksi-difusi atas domain dengan panjang L = 1 dan tunduk pada kondisi Dirichlet dari ϕ = 1 pada x = 0 dan ϕ = 0 pada x = 1. Sementara semua solusi stabil pada jumlah Péclet rendah (yaitu, Pe = 1, Figur 11.14a), solusi skema CD, FROMM, dan QUICK yang ditunjukkan dalam Figur 11.14b terlihat bergetar pada Pe = 10. Pada Pe rendah, akurasi dari skema CD dan QUICK sebanding dan solusi mereka sangat dekat dengan solusi eksak. Yang paling tidak akurat adalah solusi yang dihasilkan oleh skema upwind orde pertama. Solusi dari skema FROMM lebih akurat daripada skema SOU, yang, pada gilirannya, lebih akurat daripada solusi skema upwind, sementara kedua solusi skema FROMM dan SOU kurang akurat daripada solusi skema QUICK.
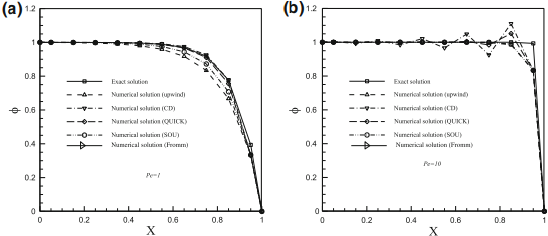
Gambar 11.14 Stabilitas solusi yang dihasilkan menggunakan beberapa skema konvektif pada dua nilai nomor Péclet sel a 1 dan b 10
Pada Pe yang tinggi, perilaku skema berubah. Satu-satunya solusi yang stabil adalah yang diperoleh dari skema upwind dan SOU dengan profil mereka hampir identik, menunjukkan bahwa skema SOU masih sangat difusif. Skema CD berombak di sebagian besar domain. Skema FROMM dan QUICK, di sisi lain, menunjukkan gelombang tetapi dengan amplitudo yang lebih kecil. Penyebab gelombang ini adalah kondisi batas yang diberlakukan saat keluar dari domain. Karena fenomena ini didominasi oleh konveksi, ia dipengaruhi oleh nilai hulu. Saat keluar dari domain, solusi menghadapi nilai yang diberlakukan yang harus dipenuhi, menyebabkan gradien besar yang tidak terduga menyebabkan terjadinya lonjakan dan celah. Skema upwind dan SOU yang difusif berdasarkan nilai hulu saja, halus dan tidak menunjukkan tanda-tanda celah untuk semua nilai Pe karena solusinya independen dari nilai yang diberlakukan saat keluar. Namun, skema SOU diharapkan menimbulkan osilasi (lonjakan/celah) dalam kehadiran gradien tinggi di domain seperti dalam kehadiran gelombang kejut.
