
Conservation and Boundedness
Conservation and Boundedness
- Pada persamaan (2.14), turunan material mencakup istilah
 . Namun, istilah ini dapat memiliki bentuk
. Namun, istilah ini dapat memiliki bentuk 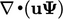 , dengan menerapkan hukum konservasi massa pada persamaan (2.8), seperti yang ditunjukkan pada bagian 2.8. Kedua istilah ini terkait oleh aturan perkalian.
, dengan menerapkan hukum konservasi massa pada persamaan (2.8), seperti yang ditunjukkan pada bagian 2.8. Kedua istilah ini terkait oleh aturan perkalian.
- Ketika dua istilah
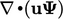 dan
dan 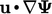 Nampak serupa namun mempengaruhi solusi suatu persamaan dengan cara yang berbeda
Nampak serupa namun mempengaruhi solusi suatu persamaan dengan cara yang berbeda
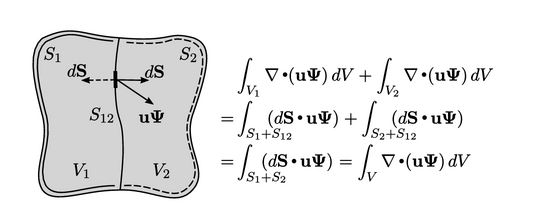
- Istilah
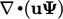 menjaga konservasi dalam
menjaga konservasi dalam 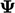 . Semua variabel berada di dalam (di sebelah kanan) divergensi
. Semua variabel berada di dalam (di sebelah kanan) divergensi 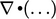 sehingga ketika kita mengintegrasikannya di atas selalu volume V, dapat sepenuhnya diubah oleh teorema Gauss menjadi dari fluks
sehingga ketika kita mengintegrasikannya di atas selalu volume V, dapat sepenuhnya diubah oleh teorema Gauss menjadi dari fluks 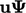 pada
pada 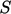 .
. - Jika kita membagi V menjadi dua sub-volume
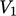 dan
dan 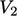 , integral permukaannya juga terbagi menjadi dua permukaan
, integral permukaannya juga terbagi menjadi dua permukaan 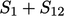 dan
dan 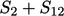 , dimana
, dimana 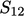 adalah bagian dari permukaan yang umum untuk kedua volume.
adalah bagian dari permukaan yang umum untuk kedua volume. - Fluks pada
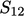 untuk setiap sub-volume memiliki magnitudo yang sama tetapi tanda yang berlawanan, karena vektor luas permukaan dS mengarah keluar dari volume ke arah yang berlawanan. Fluks ini saling membatalkan, sehingga jumlah integral di atas
untuk setiap sub-volume memiliki magnitudo yang sama tetapi tanda yang berlawanan, karena vektor luas permukaan dS mengarah keluar dari volume ke arah yang berlawanan. Fluks ini saling membatalkan, sehingga jumlah integral di atas 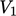 dan
dan 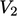 identik sama dengan integral di atas
identik sama dengan integral di atas 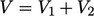 .
. - Dengan demikian, istilah
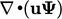 memastikan konservasi dalam
memastikan konservasi dalam 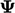 melintasi suatu permukaan yang memisahkan wilayah domain aliran. Konsevasi dijamin di semua titik pada batas
melintasi suatu permukaan yang memisahkan wilayah domain aliran. Konsevasi dijamin di semua titik pada batas 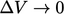 untuk setiap sub-volume.
untuk setiap sub-volume. - Bentuk (
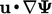 ) tidak dapat diubah menjadi integral permukaan sehingga tidak menjamin konservasi. Sebaliknya, ini memastikan terbatasnya, seperti yang ditunjukkan oleh solusi
) tidak dapat diubah menjadi integral permukaan sehingga tidak menjamin konservasi. Sebaliknya, ini memastikan terbatasnya, seperti yang ditunjukkan oleh solusi 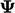 dalam persamaan berikut dalam satu dimensi (x) (1D).
dalam persamaan berikut dalam satu dimensi (x) (1D).
- Solusi persamaan ini memiliki bentuk
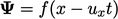 . Jika
. Jika 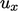 seragam, maka profil
seragam, maka profil 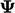 tidak berubah tetapi hanya translasi pada kecepatan
tidak berubah tetapi hanya translasi pada kecepatan 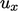 seperti yang ditunjukkan dalam diagram sebelah kiri. Jika
seperti yang ditunjukkan dalam diagram sebelah kiri. Jika 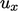 bervariasi dengan x, profil berubah, misalnya menjadi lebih datar, seperti yang ditunjukkan dalam diagram sebelah kanan.
bervariasi dengan x, profil berubah, misalnya menjadi lebih datar, seperti yang ditunjukkan dalam diagram sebelah kanan.
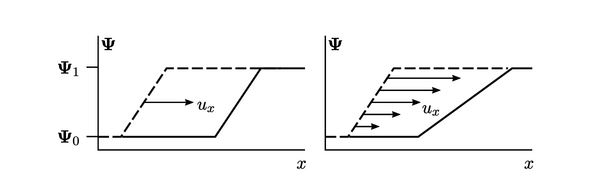
- Dalam kedua kasus tersebut, profil
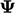 tetap berada dalam batasan asli
tetap berada dalam batasan asli 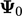 dan
dan 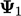 ; solusinya dikatakan terbatas. Meskipun perilakunya di ilustrasikan salam 1D, hal ini berlaku juga untuk 3D
; solusinya dikatakan terbatas. Meskipun perilakunya di ilustrasikan salam 1D, hal ini berlaku juga untuk 3D - Dengan demkian, istilah
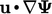 memastikan terbatasnya. Sebaliknya, istilah
memastikan terbatasnya. Sebaliknya, istilah 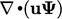 , sementara memastikan konservasi, tidak menjamin terbatasnya ketika
, sementara memastikan konservasi, tidak menjamin terbatasnya ketika 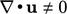 . Kedua istilah tersebut terhubung oleh
. Kedua istilah tersebut terhubung oleh 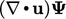 yang mengubah
yang mengubah 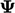 karena ekspansi/kontraksi fluida, seperti yang dibahas dalam bagian 2.4. Efeknya diilustrasikan oleh datarnya profil dalam diagram sebelah kanan, karena
karena ekspansi/kontraksi fluida, seperti yang dibahas dalam bagian 2.4. Efeknya diilustrasikan oleh datarnya profil dalam diagram sebelah kanan, karena 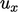 yang tidak seragam berkorelasi dengan
yang tidak seragam berkorelasi dengan 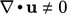 .
.
