Conservation of Mass (Continuity Equation)

Konservasi Massa (Persamaan Kontinuitas)

Conservation of mass continuity equation. Prinsip konservasi massa [6, 10] menunjukkan bahwa dalam ketiadaan sumber dan bak massa, suatu wilayah akan melestarikan massa pada tingkat lokal. Mempertimbangkan volume material fluida yang ditunjukkan dalam Gambar 3.3 dengan massa m, densitas ρ, dan kecepatan v, konservasi massa dalam sistem koordinat material (Lagrangian) dapat dituliskan sebagai

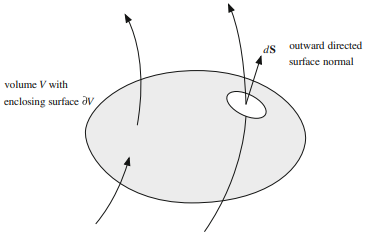
Gambar 3.3 Konservasi massa untuk volume material fluida dengan massa m

Untuk B = m, kuantitas intensif yang sesuai adalah b = 1, dan berdasarkan Persamaan (3.8), ekspresi setara dari konservasi massa dalam sistem koordinat Eulerian adalah

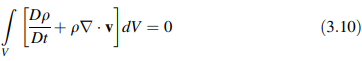
Untuk integral yang diberikan dalam Persamaan (3.10) menjadi benar untuk setiap volume kontrol V, integrannya harus sama dengan nol, memberikan bentuk diferensial dari persamaan kekekalan massa atau persamaan kontinuitas, yaitu:

Bentuk flux dari persamaan kontinuitas dapat diperoleh menggunakan Persamaan (3.7) dan menghasilkan:

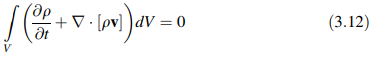
Sekali lagi, agar integral dalam Persamaan (3.12) benar untuk setiap volume kontrol V, maka integrannya harus sama dengan nol, yang memberikan bentuk flux dari persamaan kontinuitas atau kesinambungan massa sebagai:

Dalam ketiadaan perubahan tekanan atau suhu absolut yang signifikan, adalah wajar untuk mengasumsikan bahwa aliran adalah tak terkompres; artinya, perubahan tekanan tidak memiliki efek signifikan pada kerapatan. Ini hampir selalu terjadi pada cairan, dan merupakan perkiraan yang baik pada gas dengan kecepatan jauh lebih rendah dari suara. (Catatan bahwa gelombang suara adalah fenomena yang dapat terkompresi.) Konsekuensi paling penting dalam dinamika fluida adalah bahwa persamaan konservasi massa (kontinuitas) tidak lagi dapat digunakan untuk menghitung kerapatan. Kondisi tak terkompresibilitas menunjukkan bahwa q tidak berubah dengan aliran, yang secara matematis dapat diungkapkan sebagai Dρ/Dt = 0. Menggunakan persamaan konservasi massa yang diberikan oleh Persamaan (3.11), ini setara dengan mengatakan bahwa persamaan kontinuitas untuk aliran tak terkompresible diberikan oleh

atau dalam bentuk integral sebagai

Persamaan (3.15) menyatakan bahwa untuk aliran tak terkompresibel, aliran bersih melintasi setiap volume kontrol adalah nol, yaitu “aliran keluar” = “aliran masuk”. Perlu juga dicatat bahwa Dρ/Dt = 0 tidak menyiratkan bahwa ρ sama di semua tempat (meskipun hal ini terjadi pada banyak aplikasi hidrolik), tetapi bahwa ρ tidak berubah sepanjang garis arus. Untuk lebih akuratnya, pendekatan tak terkompresibilitas berarti setiap elemen fluida menjaga kerapatannya yang asli saat bergerak. Dalam praktiknya, perbedaan kerapatan umumnya dijumpai dalam air akibat variasi dalam konsentrasi garam dan dalam udara akibat perbedaan suhu yang menghasilkan gaya apungan penting.