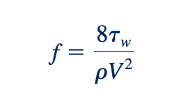Dari Analisis Dimensi
Dari analisis dimensi. Meskipun aliran laminar pipa yang sepenuhnya berkembang cukup sederhana untuk memungkinkan solusi yang cukup langsung seperti yang dibahas dalam dua bagian sebelumnya, mungkin bermanfaat untuk mempertimbangkan aliran ini dari sudut pandang analisis dimensional. Dengan demikian, kita mengasumsikan bahwa penurunan tekanan dalam pipa horizontal, Δp, adalah fungsi dari kecepatan rata-rata fluida dalam pipa, V, panjang pipa, ℓ, diameter pipa, D, dan viskositas fluida, μ, seperti yang ditunjukkan oleh gambar di pinggir. Kita tidak termasuk kepadatan atau berat jenis fluida sebagai parameter karena untuk aliran seperti ini, mereka bukan parameter penting. Tidak ada massa (kepadatan kali percepatan) atau komponen berat (berat jenis kali volume) dalam arah aliran yang terlibat. Dengan demikian,
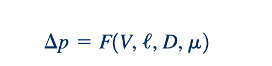
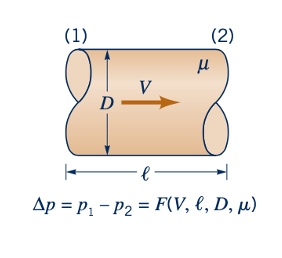
Lima variabel dapat dijelaskan dalam hal tiga dimensi referensi (M, L, T). Menurut hasil analisis dimensional (Bab 7), aliran ini dapat dijelaskan dalam hal k - r = 5 - 3 = 2 kelompok tak berdimensi. Salah satu representasi tersebut adalah:
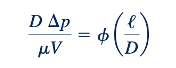
Dimana 𝜙(ℓ/𝐷) adalah fungsi yang tidak diketahui dari rasio panjang terhadap diameter pipa.
Meskipun ini adalah sejauh mana analisis dimensional bisa membawa kita, tampaknya wajar untuk memberlakukan asumsi lebih lanjut bahwa penurunan tekanan secara langsung berbanding lurus dengan panjang pipa. Artinya, diperlukan dua kali penurunan tekanan untuk memaksa fluida melalui pipa jika panjangnya digandakan. Satu-satunya cara agar ini menjadi benar adalah jika 𝜙(ℓ/𝐷) = Cℓ/D, di mana C adalah konstan. Dengan demikian, Persamaan 8.17 menjadi:
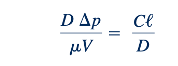
yang dapat ditulis kembali sebagai:
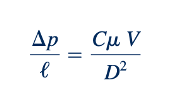
Atau
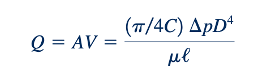
Fungsi dasar untuk aliran pipa laminar yang diberikan oleh Persamaan 8.18 sama dengan yang diperoleh dari analisis dua bagian sebelumnya. Nilai C harus ditentukan melalui teori (seperti yang dilakukan dalam dua bagian sebelumnya) atau eksperimen. Untuk pipa bundar, C=32. Untuk saluran dengan bentuk lintang yang berbeda, nilai C berbeda (lihat Bagian 8.4).
Biasanya, menggambarkan suatu proses dalam istilah kuantitas tak berdimensi bermanfaat. Untuk itu, kita mengulangi persamaan penurunan tekanan untuk aliran pipa horizontal laminar, Persamaan 8.8, sebagai Δp= 32𝜇ℓ𝑉/D2 . Kemudian, kita bagi kedua sisi dengan tekanan dinamis, ρV2/2 , untuk mendapatkan bentuk tak berdimensi sebagai.
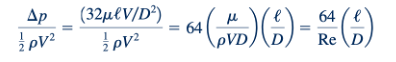
Ini sering ditulis sebagai:
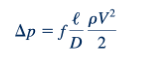
dimensi non memiliki kesatuan dan biasanya dihitung sebagai:
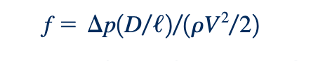
faktor gesekan, atau kadang-kadang disebut faktor gesekan Darcy [H. P. G. Darcy (1803–1858)]. Parameter ini sebaiknya tidak bingung dengan faktor gesekan Fanning yang kurang umum, yang didefinisikan sebagai f4. Dalam teks ini, kami hanya akan menggunakan faktor gesekan Darcy. Oleh karena itu, faktor gesekan untuk aliran pipa laminar yang sepenuhnya dikembangkan adalah secara sederhana,
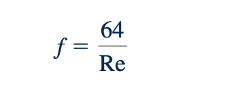
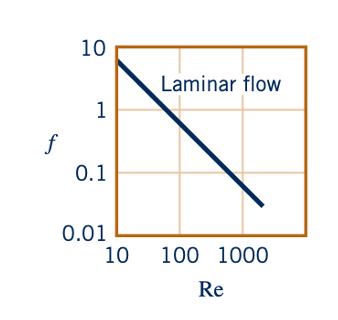
sebagaimana ditunjukkan oleh gambar di pinggiran halaman. Dengan menggantikan penurunan tekanan dalam hal tekanan geser dinding (Persamaan 8.52), kita mendapatkan ungkapan alternatif untuk faktor gesekan sebagai tekanan geser dinding yang tanpa dimensi.