Dari F = ma Diterapkan Langsung pada Elemen Fluida
Dari F = ma diterapkan langsung pada elemen fluida. Kita pertimbangkan elemen fluida pada waktu t seperti yang ditunjukkan dalam Gambar 8.7. Ini adalah silinder cairan berbentuk lingkaran dengan panjang โ dan radius r yang berpusat pada sumbu pipa horizontal berdiameter D. Karena kecepatannya tidak seragam di sepanjang pipa, ujung-ujung datar silinder cairan pada waktu t menjadi terdistorsi pada waktu t + ๐ฟt ketika elemen fluida telah bergerak ke lokasi barunya di sepanjang pipa seperti yang ditunjukkan dalam gambar. Jika aliran sepenuhnya berkembang dan stabil, distorsi pada setiap ujung elemen fluida sama, dan tidak ada bagian dari fluida yang mengalami percepatan saat mengalir, seperti yang ditunjukkan oleh gambar di margin. Percepatan lokal adalah nol (๐๐/๐๐ก=0) karena aliran adalah stabil, dan percepatan konvektif adalah nol (๐โโ ๐ =๐ข๐๐ข/๐๐ฅ ๐=0) karena aliran sepenuhnya berkembang. Dengan demikian, setiap bagian dari fluida hanya mengalir sepanjang garis alirnya sejajar dengan dinding pipa dengan kecepatan konstan, meskipun partikel tetangga memiliki kecepatan yang sedikit berbeda. Kecepatan bervariasi dari satu garis aliran ke garis aliran berikutnya. Variasi kecepatan ini, yang digabungkan dengan viskositas fluida, menghasilkan gaya geser.
Jika efek gravitasi diabaikan, tekanan adalah konstan di setiap potongan melintang vertikal pipa, meskipun bervariasi sepanjang pipa dari satu bagian ke bagian berikutnya. Dengan demikian, jika tekanannya adalah p pada bagian (1), maka tekanannya pada bagian (2) adalah p2 = p1 - ฮp, di mana ฮp adalah penurunan tekanan antara bagian (1) dan (2). Kami mengantisipasi bahwa tekanan menurun ke arah aliran sehingga ฮp โค 0. Sebuah gaya geser, t, bekerja pada permukaan silinder fluida. Stres viskos ini adalah fungsi dari radius silinder, t = t1r^2.
Seperti yang dilakukan dalam analisis statika fluida (Bab 2), kita mengisolasi silinder fluida seperti yang ditunjukkan dalam Gambar 8.8 dan menerapkan hukum kedua Newton, Fx = max. Dalam kasus ini, meskipun fluida bergerak, ia tidak berakselerasi, sehingga ax = 0. Dengan demikian, aliran pipa horizontal sepenuhnya berkembang hanyalah sebuah
keseimbangan antara gaya tekanan dan gaya viskosโperbedaan tekanan yang bertindak pada ujung silinder dengan luas ๐r^2, dan gaya geser yang bertindak pada permukaan lateral silinder dengan luas 2๐rโ. Keseimbangan gaya ini dapat dituliskan sebagai
yang dapat disederhanakan menjadi
Persamaan 8.3 mewakili keseimbangan dasar dalam gaya yang diperlukan untuk mendorong setiap partikel fluida sepanjang pipa dengan kecepatan konstan. Karena baik โ๐ maupun โ tidak merupakan fungsi dari koordinat radial, r, maka haruslah 2๐/r juga tidak tergantung pada r. Artinya, ๐= Cr, di mana C adalah konstanta. Pada r= 0 (pusat pipa) tidak ada gaya geser (๐ =0). Pada r = D/2 (dinding pipa) gaya geser mencapai maksimum, disimbolkan dengan ๐w, gaya geser dinding. Oleh karena itu, C = 2๐w/D dan distribusi gaya geser sepanjang pipa adalah fungsi linear dari koordinat radial.
seperti yang terindikasi dalam Gambar 8.9. Ketergantungan linear ๐ terhadap r merupakan hasil dari gaya tekanan yang berbanding lurus dengan r2 (tekanan bertindak pada ujung silinder fluida; luasnya =๐r2) dan gaya geser yang berbanding lurus dengan r (gayag geser bertindak pada sisi lateral silinder; luasnya 2๐r/2). Jika viskositasnya nol, tidak akan ada gaya geser, dan tekanan akan konstan di seluruh pipa horizontal (โ๐ = 0). Seperti yang terlihat dari Persamaan 8.3 dan 8.4, penurunan tekanan dan gaya geser dinding berkaitan dengan persamaan:
Gaya geser kecil dapat menghasilkan perbedaan tekanan yang besar jika pipa relatif panjang (โ/D โซ 1).
Meskipun kita sedang membahas aliran laminar, pertimbangan lebih dekat terhadap asumsi yang terlibat dalam derivasi Persamaan 8.3, 8.4, dan 8.5 mengungkapkan bahwa persamaan-persamaan ini berlaku baik untuk aliran laminar maupun turbulent. Untuk meneruskan analisis, kita harus menentukan bagaimana hubungan antara gaya geser dan kecepatan. Ini adalah langkah kritis yang memisahkan analisis aliran laminar dari aliran turbulenโdari kemampuan untuk memecahkan sifat aliran laminar dan tidak bisa memecahkan sifat aliran turbulen tanpa asumsi tambahan yang diperlukan. Seperti yang dibahas dalam Bagian 8.3, ketergantungan gaya geser untuk aliran turbulen sangat kompleks. Namun, untuk aliran laminar dari suatu
Untuk fluida Newtonian, gaya geser secara sederhana berbanding lurus dengan gradien kecepatan, "๐ = ๐ du/dy" (lihat Bagian 1.62). Dalam notasi yang terkait dengan aliran pipa kita, ini menjadi:
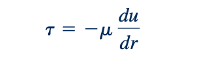
Tanda negatif dimasukkan untuk memberikan ๐ > 0 dengan du/dr = 0 (kecepatan berkurang dari garis tengah pipa ke dinding pipa).
Persamaan 8.3 dan 8.6 mewakili dua hukum yang mengatur aliran laminar yang sepenuhnya berkembang dari fluida Newtonian dalam pipa horizontal. Satu adalah hukum kedua Newton tentang gerak, dan yang lainnya adalah definisi fluida Newtonian. Dengan menggabungkan kedua persamaan ini, kita mendapatkan:
yang dapat diintegrasikan untuk memberikan profil kecepatan sebagai berikut:
Atau
dimana C1 adalah konstanta. Karena fluida bersifat kental, ia menempel pada dinding pipa sehingga u = 0 pada r = D/2. Dengan demikian, C1= (โ๐/16๐โ)D . Oleh karena itu, profil kecepatan dapat ditulis sebagai
dimana Vc = โ๐D2/(16๐โ) adalah kecepatan garis tengah. Ekspresi alternatif dapat ditulis dengan menggunakan hubungan antara tegangan geser dinding dan gradien tekanan (Eqs. 8.5 dan 8.7) untuk memberikan
di mana R= D/2 adalah jari-jari pipa.
Profil kecepatan ini, digambarkan dalam Gambar 8.9, bersifat parabola dalam koordinat radial, r, memiliki kecepatan maksimum, Vc , di garis tengah pipa, dan kecepatan minimum (nol) di dinding pipa. Debit volume melalui pipa dapat diperoleh dengan mengintegrasikan profil kecepatan di sepanjang pipa. Karena aliran bersifat simetris terhadap garis tengah, kecepatan konstan pada elemen area kecil yang terdiri dari cincin dengan jari-jari r dan ketebalan dr, seperti yang ditunjukkan dalam gambar di samping. Dengan demikian,
Atau
Menurut definisi, kecepatan rata-rata adalah debit aliran dibagi oleh luas penampang, V= Q/A=Q/ ฯR2 , sehingga untuk aliran ini
Dan
Untuk profil kecepatan dengan bentuk lain (seperti pada aliran pipa turbulen), kecepatan rata-rata bukanlah hanya rata-rata dari kecepatan maksimum (Vc) dan minimum (0) seperti pada profil parabolik laminar. Dua profil kecepatan yang terindikasi dalam Gambar 8.9 memberikan debit aliran yang sama โ satu adalah profil ideal fiktif (๐=0), yang lainnya adalah profil aliran laminar aktual.
Hasil di atas mengonfirmasi beberapa sifat aliran pipa laminar. Untuk pipa horizontal, debit aliran (a) secara langsung berbanding lurus dengan penurunan tekanan, (b) berbanding terbalik dengan viskositas, (c) berbanding terbalik dengan panjang pipa, dan (d) berbanding lurus dengan diameter pipa pangkat empat. Dengan semua parameter lain tetap, peningkatan diameter sebesar faktor 2 akan meningkatkan debit aliran sebesar faktor 2(4) = 16โdebit aliran sangat tergantung pada ukuran pipa. Ketergantungan ini ditunjukkan oleh gambar di pinggir. Demikian pula, kesalahan kecil dalam diameter pipa dapat menyebabkan kesalahan yang relatif besar dalam debit aliran. Sebagai contoh, kesalahan 2% dalam diameter akan memberikan kesalahan 8% dalam debit aliran (Q ~ D4 atau ๐ฟQ~4D(3) ๐ฟD), sehingga ๐ฟQ/Q=4๐ฟD/D. Aliran ini, sifatnya pertama kali ditetapkan secara eksperimental oleh dua peneliti independen, G. Hagen (1797โ1884) pada tahun 1839 dan J. Poiseuille (1799โ1869) pada tahun 1840, disebut aliran Hagen-Poiseuille. Persamaan 8.9 umumnya disebut hukum Poiseuille. Ingat bahwa semua hasil ini terbatas pada aliran laminar (dengan jumlah Reynolds kurang dari sekitar 2100) dalam pipa horizontal.
Penyesuaian yang diperlukan untuk memperhitungkan pipa yang tidak horizontal, seperti yang ditunjukkan dalam Gambar 8.10, dapat dengan mudah dimasukkan dengan mengganti penurunan tekanan, ฮp, oleh efek gabungan tekanan dan gravitasi, ฮp= ๐พโ sinฮธ , di mana ฮธ adalah sudut antara pipa dan horizontal. (Perhatikan bahwa ฮธ>0 jika aliran naik, sedangkan ฮธ<0 jika aliran menurun.) Ini dapat dilihat dari keseimbangan gaya dalam arah x (sepanjang sumbu pipa) pada silinder fluida yang ditunjukkan dalam Gambar 8.10b. Metode ini sama persis dengan yang digunakan untuk mendapatkan persamaan Bernoulli (Persamaan 3.62) ketika garis aliran tidak horizontal. Gaya bersih dalam arah x adalah kombinasi dari gaya tekanan dalam arah tersebut, ฮpฯr2 , dan komponen berat dalam arah tersebut, -๐พฯr โ sinฮธ. Hasilnya adalah bentuk sedikit dimodifikasi dari Persamaan 8.3 yang diberikan oleh
Oleh karena itu, semua hasil untuk pipa horizontal tetap valid dengan asumsi gradien tekanan disesuaikan untuk suku elevasi, yaitu, ฮp diganti dengan ฮp - ๐พโ sinฮธ , sehingga
Dan
Diperhatikan bahwa gaya penggerak untuk aliran pipa bisa jadi adalah penurunan tekanan ke arah aliran, ฮp, atau komponen dari berat ke arah aliran, -๐พโ sinฮธ . Jika aliran menuruni, gravitasi membantu aliran (diperlukan penurunan tekanan yang lebih kecil; sinฮธ< 0.2). Jika aliran menanjak, gravitasi bertentangan dengan aliran (diperlukan penurunan tekanan yang lebih besar; sinฮธ>0.2). Perlu diperhatikan bahwa ๐พโ sinฮธ adalah ๐พฮz (di mana ฮz menyatakan perubahan ketinggian).ฮz adalah perubahan ketinggian, merupakan istilah tekanan tipe hidrostatik. Jika tidak ada aliran, V=0 dan ฮp= ๐พโ sinฮธ =๐พฮz, seperti yang diharapkan untuk fluida statis.
