Data Koefisien Tarik dan Contohnya
Data koefisien tarik dan contohnya. Seperti yang dibahas dalam bagian-bagian sebelumnya, drag bersih dihasilkan oleh efek tekanan dan gaya geser. Dalam kebanyakan kasus, kedua efek ini dipertimbangkan bersama, dan koefisien drag keseluruhan, CD, seperti yang didefinisikan dalam Persamaan 9.36 digunakan. Ada banyak data koefisien drag seperti ini yang tersedia dalam literatur. Informasi ini mencakup aliran kental tak terkompresibel dan terkompresibel melintasi objek dengan hampir semua bentuk yang menarik perhatian—baik objek buatan manusia maupun alam. Dalam bagian ini, kita mempertimbangkan sebagian kecil dari informasi tersebut untuk situasi representatif. Data tambahan dapat diperoleh dari berbagai sumber.
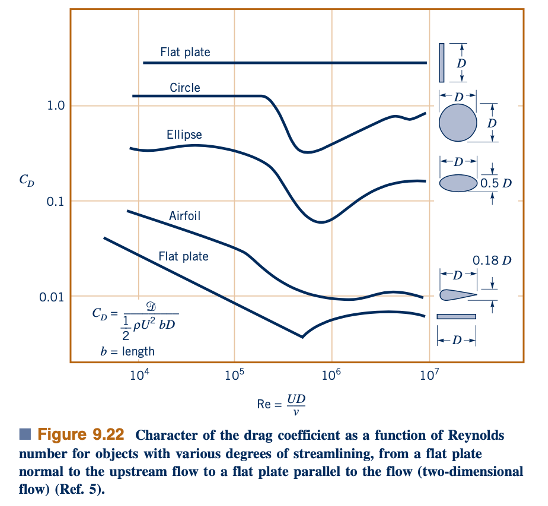
Ketergantungan pada Bentuk. Jelas, koefisien drag untuk sebuah objek tergantung pada bentuk objek tersebut, dengan bentuk-bentuk mulai dari yang aerodinamis hingga yang tumpul. Drag pada sebuah elips dengan rasio aspek ℓ/𝐷, di mana D dan ℓ adalah ketebalan dan panjang sejajar aliran, mengilustrasikan ketergantungan ini. Koefisien drag CD =𝔇(pU2 bD/2), berdasarkan area frontal, A =bD, di mana b adalah panjang tegak lurus terhadap aliran, seperti yang ditunjukkan dalam Gambar 9.19. Semakin tumpul bentuk tubuhnya, semakin besar koefisien dragnya. Dengan ℓ/𝐷= 0 (yaitu, sebuah plat datar tegak lurus terhadap aliran), kita mendapatkan nilai plat datar dari CD 1.9. Dengan ℓ/𝐷= 1, nilai yang sesuai untuk sebuah silinder berbentuk lingkaran diperoleh. Saat ℓ/𝐷 semakin besar, nilai CD semakin menurun.
Untuk rasio aspek yang sangat besar (ℓ/𝐷 → ∞), elips berperilaku seperti plat datar sejajar aliran. Untuk kasus-kasus seperti itu, drag gesekan lebih besar daripada drag tekanan, dan nilai CD berdasarkan area depan, A = bD, akan meningkat dengan meningkatnya ℓ/𝐷. (Ini terjadi untuk nilai ℓ/𝐷 yang lebih besar daripada yang ditunjukkan dalam gambar.) Untuk tubuh yang sangat tipis seperti itu (yaitu, sebuah elips dengan ℓ/𝐷 → ∞ , sebuah plat datar, atau airfoil yang sangat tipis), umumnya digunakan area rencana, A = bℓ, dalam mendefinisikan koefisien drag.
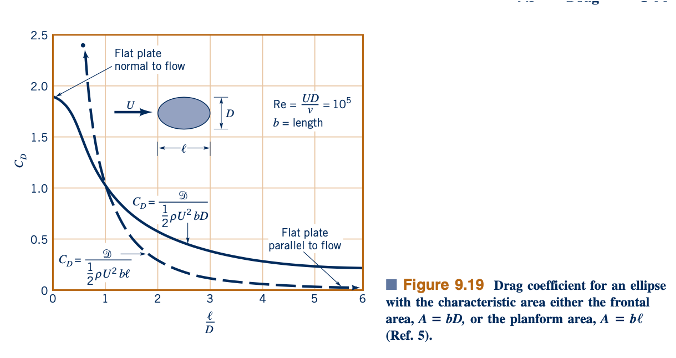
Akhirnya, ini adalah area rencana di mana tegangan geser bekerja, bukan area depan yang jauh lebih kecil (untuk tubuh tipis). Koefisien drag elips berdasarkan area rencana, C = 𝔇/(pU2bℓ/2), juga ditunjukkan dalam Gambar 9.19. Jelas bahwa drag yang diperoleh dengan menggunakan salah satu koefisien drag ini akan sama. Mereka hanya mewakili dua cara yang berbeda untuk mengemas informasi yang sama.
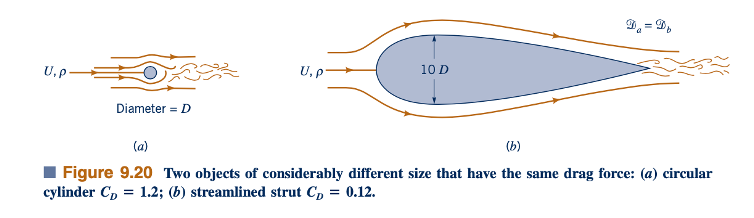
Jumlah streamlining dapat memiliki efek yang signifikan pada drag. Dengan luar biasa, drag pada dua objek dua dimensi yang digambar dengan skala dalam Gambar 9.20 adalah sama. Lebar bangun untuk strut yang aerodinamis sangat tipis, sekitar pada tingkat yang sama dengan silinder lingkaran yang jauh lebih kecil.
Ketergantungan pada Reynolds number. Parameter lain yang sangat memengaruhi koefisien drag adalah Reynolds number. Kategori utama ketergantungan Reynolds number adalah 1) aliran Reynolds number sangat rendah, 2) aliran Reynolds number sedang (lapisan batas laminar), dan 3) aliran Reynolds number sangat tinggi (lapisan batas turbulen). Contoh dari ketiga situasi ini dibahas di bawah ini.
Aliran Reynolds number sangat rendah (Re < 1) dikuasai oleh keseimbangan antara gaya viscous dan tekanan. Efek inersia sangat kecil. Dalam kasus seperti itu, drag pada suatu tubuh tiga dimensi diharapkan menjadi fungsi dari kecepatan aliran, U, ukuran tubuh, ℓ, dan viskositas, 𝜇. Oleh karena itu, untuk butiran pasir kecil yang tenggelam di danau (lihat gambar di pinggir)

Dari pertimbangan dimensional (lihat Bagian 7.7.12)
jika kita memasukkan Persamaan 9.38 ke dalam bentuk tak berdimensi menggunakan definisi standar dari koefisien drag, kita mendapatkan
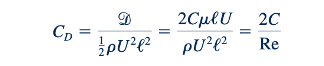
di mana Re= pUℓ/𝜇. Penggunaan tekanan dinamis, rU22, dalam definisi koefisien drag agak menyesatkan dalam kasus aliran merayap (Re<1) karena hal ini memperkenalkan
Itu adalah suatu konvensi bahwa penggunaan drag coefficient yang didefinisikan secara standar memberikan ketergantungan 1/Re untuk drag yang kecil.
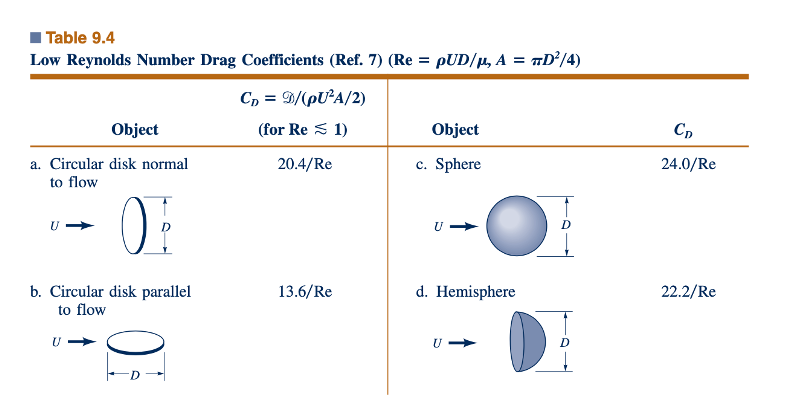
Nilai tipikal CD untuk aliran dengan Reynolds number rendah melalui berbagai objek diberikan dalam Tabel 9.4. Menarik untuk dicatat bahwa drag pada sebuah cakram tegak lurus terhadap aliran hanya 1,5 kali lebih besar dari pada cakram sejajar dengan aliran. Untuk aliran dengan Reynolds number besar, rasio ini jauh lebih besar. Merancang sebuah objek agar lebih aerodinamis (misalnya, membuat objek menjadi lebih ramping) dapat menghasilkan penurunan drag yang signifikan untuk aliran dengan Reynolds number besar; untuk aliran dengan Reynolds number yang sangat kecil, hal ini sebenarnya dapat meningkatkan drag karena peningkatan area di mana gaya gesekan bertindak. Untuk sebagian besar objek, hasil dari aliran dengan Reynolds number rendah berlaku hingga sekitar Reynolds number 1.

Aliran dengan Reynolds number sedang cenderung mengambil struktur aliran lapisan batas. Untuk aliran semacam itu melalui benda-benda yang aerodinamis, koefisien drag cenderung sedikit berkurang dengan Reynolds number. Ketergantungan CD ~ Re^-1/2 untuk lapisan batas laminar pada plat datar adalah contoh dari hal ini. Aliran dengan Reynolds number sedang melalui benda-benda tumpul umumnya menghasilkan koefisien drag yang relatif konstan. Nilai CD untuk bola dan silinder berbentuk lingkaran yang ditunjukkan pada Gambar 9.21a menunjukkan karakter ini dalam rentang 10^3 < Re < 10^5.
Struktur medan aliran pada Reynolds number tertentu yang ditunjukkan pada Gambar 9.21a ditunjukkan pada Gambar 9.21b. Untuk sebuah objek tertentu, ada berbagai situasi aliran yang beragam, tergantung pada Reynolds number yang terlibat. Pembaca yang ingin tahu lebih lanjut sangat dianjurkan untuk mempelajari banyak foto dan video yang indah dari situasi aliran ini yang ditemukan di Referensi 8 dan 31. (Lihat juga foto di awal Bab 7.)
Untuk banyak bentuk, ada perubahan mendadak dalam karakter koefisien drag ketika lapisan batas menjadi turbulen. Hal ini diilustrasikan dalam Gambar 9.15 untuk plat datar dan dalam Gambar 9.21 untuk bola dan silinder berbentuk lingkaran. Reynolds number di mana transisi ini terjadi merupakan fungsi dari bentuk benda.
Untuk benda-benda aerodinamis, koefisien drag meningkat ketika lapisan batas menjadi turbulen karena sebagian besar drag disebabkan oleh gaya gesek, yang lebih besar untuk aliran turbulen daripada aliran laminar. Di sisi lain, koefisien drag untuk benda yang relatif tumpul, seperti silinder atau bola, sebenarnya menurun ketika lapisan batas menjadi turbulen. Seperti yang dibahas di Bagian 9.2.6, lapisan batas turbulen dapat bergerak lebih jauh sepanjang permukaan ke dalam gradien tekanan yang tidak menguntungkan.
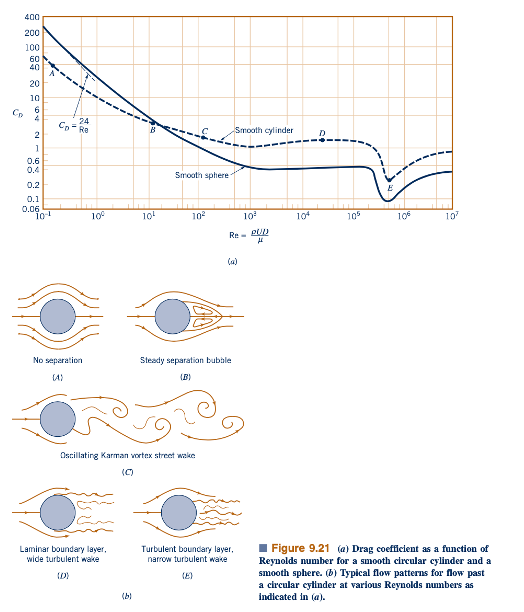
gradien tekanan di bagian belakang silinder sebelum terjadinya pemisahan. Hasilnya adalah alur yang lebih tipis dan drag tekanan yang lebih kecil untuk aliran lapisan batas turbulen. Ini ditunjukkan dalam Gambar 9.21 oleh penurunan tiba-tiba pada CD untuk 10^5 < Re < 10^6. Dalam sebagian dari rentang ini, drag aktual (bukan hanya koefisien drag) menurun dengan peningkatan kecepatan. Sangat sulit untuk mengendalikan penerbangan stabil objek di rentang ini - peningkatan kecepatan memerlukan penurunan dorong (drag). Pada semua rentang Reynolds number lainnya, drag meningkat dengan peningkatan kecepatan aliran masuk (meskipun CD dapat menurun dengan Re).
Untuk benda yang sangat tumpul, seperti sebuah plat datar tegak lurus terhadap aliran, aliran terpisah pada tepi plat tidak peduli dengan sifat aliran lapisan batas. Oleh karena itu, koefisien drag menunjukkan sedikit ketergantungan pada nomor Reynolds.
Koefisien drag untuk serangkaian benda dua dimensi dengan berbagai tingkat tumpulnya diberikan sebagai fungsi dari nomor Reynolds dalam Gambar 9.22. Karakteristik yang dijelaskan di atas terlihat jelas.

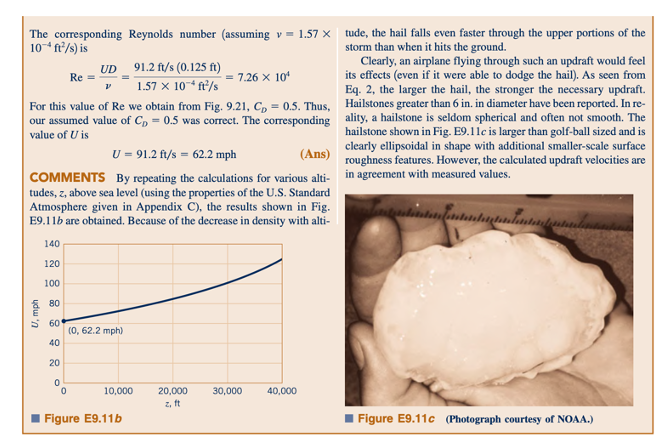
Efek Kompresibilitas. Pembahasan di atas terbatas pada aliran tak terkompresibel. Jika kecepatan benda cukup besar, efek kompresibilitas menjadi penting, dan koefisien drag menjadi fungsi dari nomor Mach, Ma=U/c, di mana c adalah kecepatan suara dalam fluida. Pengenalan efek nomor Mach mempersulit masalah karena koefisien drag untuk benda tertentu kemudian menjadi fungsi dari kedua nomor Reynolds dan nomor Mach - CD = 𝜙(Re, Ma). Efek nomor Mach dan Reynolds seringkali terhubung erat karena keduanya sebanding langsung dengan kecepatan hulu. Misalnya, baik Re maupun Ma meningkat dengan peningkatan kecepatan terbang pesawat. Perubahan dalam CD karena perubahan U disebabkan oleh perubahan baik Re maupun Ma.
Ketergantungan yang tepat dari koefisien drag terhadap Re dan Ma pada umumnya cukup kompleks. Namun, penyederhanaan berikut sering kali bisa diterima. Untuk nilai Mach yang rendah, koefisien drag pada dasarnya independen dari Ma seperti yang terindikasi dalam Gambar 9.23. Untuk situasi ini, jika Ma 6 0.5
atau sekitarnya, efek kompresibilitas tidak penting. Di sisi lain, untuk aliran dengan nomor Mach yang lebih besar, koefisien drag dapat sangat tergantung pada Ma, dengan efek nomor Reynolds hanya sekunder.
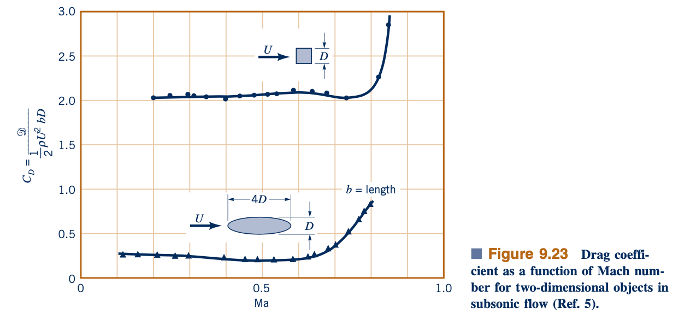
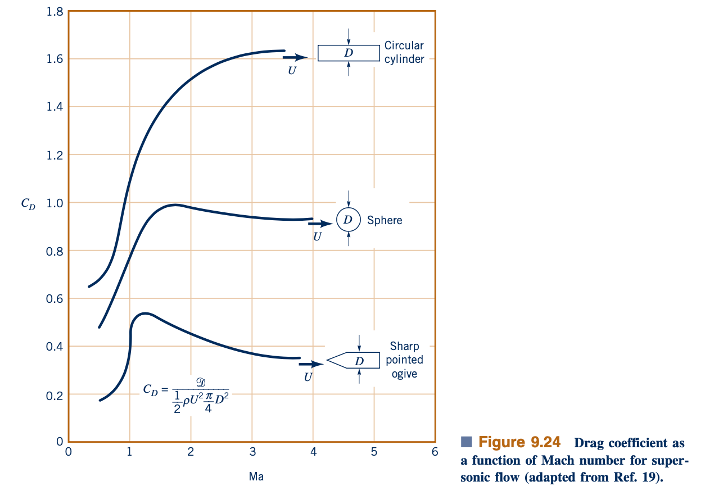
Untuk sebagian besar objek, nilai-nilai CD meningkat secara dramatis di sekitar Ma = 1 (yaitu, aliran sonic). Perubahan karakter ini, seperti yang ditunjukkan oleh Gambar 9.24, disebabkan oleh adanya gelombang kejut seperti yang ditunjukkan oleh gambar di sisi margin. Gelombang kejut adalah wilayah yang sangat sempit dalam medan aliran di mana parameter aliran berubah secara hampir diskontinu, yang dibahas dalam Bab 11. Gelombang kejut, yang tidak dapat ada dalam aliran subsonik, memberikan mekanisme untuk pembangkitan drag yang tidak hadir dalam aliran subsonik yang relatif rendah kecepatannya. (Lihat foto di awal Bab 11.)
Karakter koefisien drag sebagai fungsi dari bilangan Mach berbeda untuk benda tumpul daripada benda runcing. Seperti yang ditunjukkan dalam Figur 9.24, benda-benda tajam cenderung memiliki koefisien drag maksimumnya di sekitar Ma = 1 (aliran sonik), sedangkan koefisien drag untuk benda tumpul meningkat dengan Ma jauh di atas Ma = 1. Perilaku ini disebabkan oleh struktur gelombang kejut dan pemisahan aliran yang menyertainya. Tepi-tepi depan sayap untuk pesawat subsonik biasanya cukup bulat dan tumpul, sementara yang untuk pesawat supersonik cenderung sangat tajam. Informasi lebih lanjut tentang topik penting ini dapat ditemukan dalam teks standar tentang aliran kompresibel dan aerodinamika (lihat Referensi 9, 10, dan 29).
Kasaran Permukaan. Seperti yang ditunjukkan dalam Figur 9.15, drag pada plat datar sejajar dengan aliran sangat bergantung pada kasaran permukaan, asalkan aliran lapisan batas turbulen. Dalam kasus tersebut, kasaran permukaan menonjol melalui lapisan batas laminar yang berdekatan dengan permukaan (lihat Bagian 8.42) dan mengubah tekanan geser dinding. Selain peningkatan tekanan geser turbulen, kasaran permukaan juga dapat mengubah bilangan Reynolds di mana aliran lapisan batas menjadi turbulen. Oleh karena itu, plat datar kasar mungkin memiliki bagian yang lebih besar dari panjangnya tertutup oleh lapisan batas turbulen daripada plat halus yang sesuai. Ini juga bertindak untuk meningkatkan drag bersih pada plat.
Pada umumnya, untuk benda-benda yang aerodinamis, drag meningkat seiring dengan peningkatan kasaran permukaan. Perhatian besar diberikan untuk merancang permukaan sayap pesawat terbang agar sesuai dengan yang halus mungkin, karena penonjolan rivet atau kepala sekrup dapat menyebabkan peningkatan drag yang signifikan. Di sisi lain, untuk benda yang sangat tumpul, seperti plat datar normal terhadap aliran, drag tidak tergantung pada kasaran permukaan, karena gaya geser tidak searah dengan aliran utama dan tidak memberikan kontribusi apa pun terhadap drag.
Untuk benda-benda tumpul seperti silinder lingkaran atau bola, peningkatan kasaran permukaan sebenarnya dapat menyebabkan penurunan drag. Hal ini diilustrasikan untuk bola dalam Figur 9.25. Seperti yang dibahas dalam Bagian 9.2.6, ketika bilangan Reynolds mencapai nilai kritis (Re = 3 × 10^5) untuk permukaan yang halus,
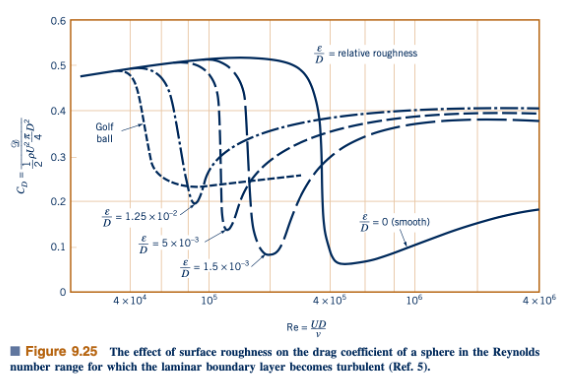
dan wilayah bangun belakang bola menjadi jauh lebih sempit dibandingkan jika itu laminar (lihat Gambar 9.172). Akibatnya, terjadi penurunan yang signifikan dalam drag tekanan dengan sedikit peningkatan drag gesekan, yang menggabungkan untuk memberikan drag keseluruhan yang lebih kecil (dan CD).
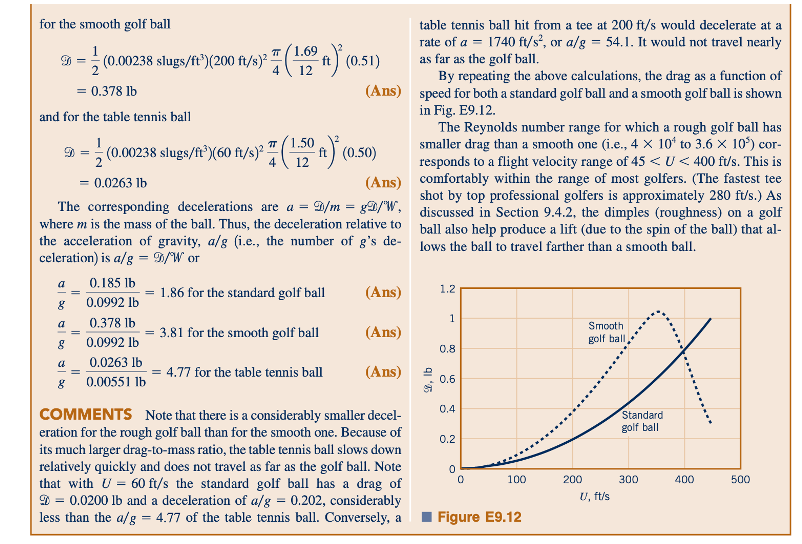
Lapisan batas dapat dipaksa menjadi turbulen pada bilangan Reynolds yang lebih kecil dengan menggunakan bola yang berpermukaan kasar. Sebagai contoh, bilangan Reynolds kritis untuk bola golf adalah sekitar Re = 4 × 10^4. Dalam rentang 4 × 10^4 ≤ Re ≤ 4 × 10^5, drag pada bola golf yang berpermukaan kasar (yaitu, berlekuk) jauh lebih rendah (CD kasar = CD halus × 0,25 ≈ 0,5 × 0,52) daripada pada bola yang halus. Seperti yang ditunjukkan dalam Contoh 9.12, ini tepatnya rentang bilangan Reynolds untuk bola golf yang terpukul dengan baik—sehingga, alasan untuk lekukan pada bola golf. Rentang bilangan Reynolds untuk bola tenis meja yang terpukul dengan baik adalah kurang dari Re = 4 × 10^4. Oleh karena itu, bola tenis meja adalah halus.

Bilangan Froude. Parameter lain yang dragnya mungkin sangat tergantung adalah bilangan Froude, Fr = U / √(gD). Seperti yang dibahas dalam Bab 10, bilangan Froude adalah rasio kecepatan aliran bebas terhadap kecepatan gelombang tipikal pada antarmuka dua fluida, seperti permukaan laut. Benda yang bergerak di permukaan, seperti kapal, seringkali menghasilkan gelombang yang memerlukan sumber energi untuk dibentuk. Energi ini berasal dari kapal dan termanifestasi sebagai drag. [Ingat bahwa laju produksi energi (daya) sama dengan kecepatan dikali gaya.] Karakter gelombang yang dihasilkan seringkali bergantung pada bilangan Froude aliran dan bentuk benda—gelombang yang dihasilkan oleh pemain ski air yang "membelah" air dengan kecepatan rendah (Fr rendah) berbeda dengan yang dihasilkan oleh pemain ski yang "membentang" di permukaan dengan kecepatan tinggi (Fr besar).
Oleh karena itu, koefisien drag untuk kapal permukaan adalah fungsi dari bilangan Reynolds (efek viskos) dan bilangan Froude (efek pembentukan gelombang); CD = f(Re, Fr). Seperti yang dibahas dalam Bab 7, seringkali cukup sulit untuk melakukan uji model di bawah kondisi yang mirip dengan prototipe (yaitu, Re dan Fr yang sama untuk kapal permukaan). Untungnya, efek viskos dan gelombang seringkali dapat dipisahkan, dengan total drag merupakan jumlah drag dari efek-efek ini secara individual. Penjelasan detail tentang topik penting ini dapat ditemukan dalam teks standar.
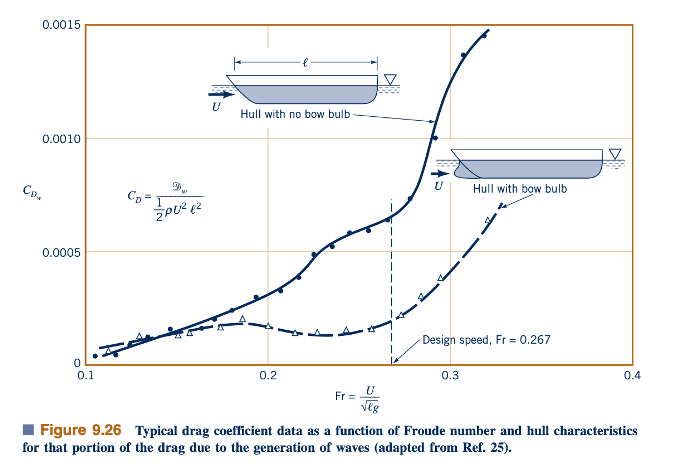
CDw = 𝔇w/(pU^2 ℓ^2/2), pada bilangan Froude yang ditunjukkan adalah tipikal. Ini disebabkan oleh struktur gelombang yang dihasilkan oleh lambung kapal yang merupakan fungsi kuat dari kecepatan kapal atau, dalam bentuk tak berdimensi, bilangan Froude. Struktur gelombang ini juga merupakan fungsi dari bentuk badan kapal. Misalnya, gelombang haluan, yang seringkali menjadi penyumbang utama terhadap drag gelombang, dapat dikurangi dengan menggunakan tonjolan yang didesain secara tepat pada bagian haluan, seperti yang ditunjukkan dalam Gambar 9.26. Dalam kasus ini, tubuh yang memiliki bentuk aliran (lambung tanpa tonjolan) memiliki lebih banyak drag dibandingkan dengan yang kurang aliran.
Drag Tubuh Gabungan. Perhitungan drag perkiraan untuk tubuh kompleks seringkali dapat diperoleh dengan memperlakukan tubuh sebagai koleksi komposit dari berbagai bagian. Sebagai contoh, gaya total pada tiang bendera karena angin (lihat gambar di pinggiran) dapat diperkirakan dengan menambahkan drag aerodinamis yang dihasilkan oleh berbagai komponen yang terlibat—drag pada bendera dan drag pada tiang. Dalam beberapa kasus, perhatian yang besar harus diberikan dalam pendekatan seperti ini karena interaksi antara berbagai bagian. Mungkin tidak benar untuk hanya menambahkan drag dari komponen-komponen untuk mendapatkan drag dari keseluruhan objek, meskipun pendekatan-pendekatan semacam itu seringkali wajar.


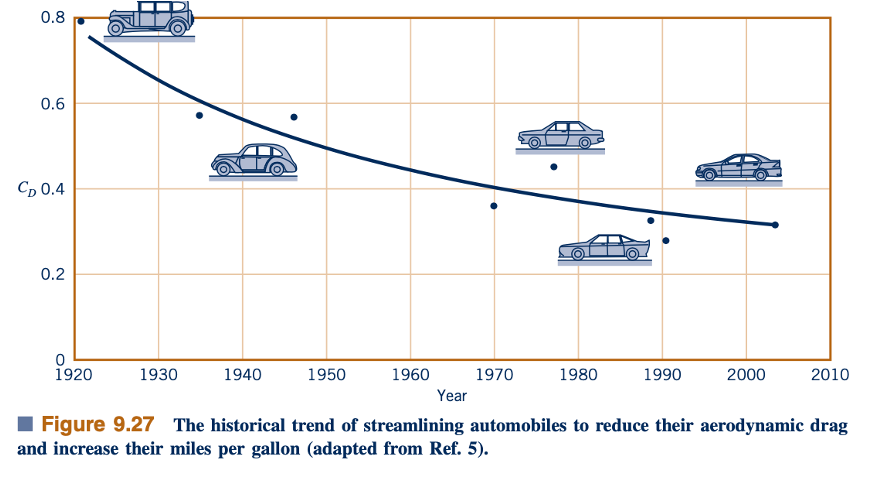
perhitungan komputasi. Berbagai komponen tersebut dapat diperkirakan memiliki kontribusi drag yang berbeda terhadap total drag aerodinamis dari mobil. Dalam perancangan mobil modern, pengurangan drag aerodinamis menjadi fokus utama untuk meningkatkan efisiensi bahan bakar dan kinerja keseluruhan.
Dalam banyak kasus, pengurangan drag aerodinamis telah dicapai melalui penggunaan desain yang lebih aerodinamis, seperti kurva dan kontur yang disesuaikan secara cermat untuk mengalirkan udara dengan lebih lancar di sekitar mobil. Selain itu, fitur-fitur aerodinamis tambahan seperti spoiler, splitter, dan diffuser juga digunakan untuk mengelola aliran udara di sekitar mobil dan mengurangi drag aerodinamis. Teknologi canggih seperti simulasi aliran fluida komputasi (CFD) juga digunakan untuk memodelkan dan mengoptimalkan desain aerodinamis mobil sebelum produksi fisik dimulai.