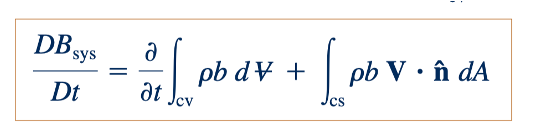Derivasi Teorema Transport Reynolds
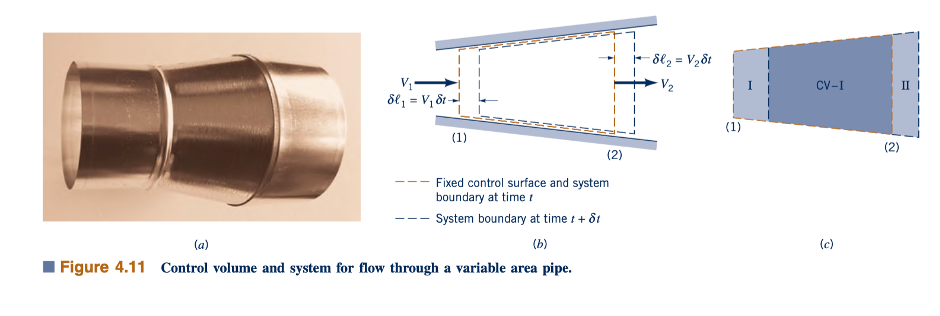
Derivasi Teorema Transport Reynolds. Versi sederhana dari teorema transportasi Reynolds yang menghubungkan konsep sistem dengan konsep volume kontrol dapat diperoleh dengan mudah untuk aliran satu dimensi melalui volume kontrol tetap seperti bagian saluran duct variabel yang ditunjukkan dalam Gambar 4.11a. Kita anggap volume kontrol sebagai volume diam dalam saluran duct antara bagian (1) dan (2) seperti yang ditunjukkan dalam Gambar 4.11b. Sistem yang kita pertimbangkan adalah fluida yang mengisi volume kontrol pada suatu waktu awal t. Beberapa waktu kemudian, pada waktu t + 𝛿t, sistem telah bergerak sedikit ke kanan. Partikel-fluida yang bertepatan dengan bagian (2) dari permukaan kontrol pada waktu t telah bergerak sejauh 𝜕ℓ2/V2 𝜕t ke kanan, di mana V2 adalah kecepatan fluida saat melewati bagian (2). Demikian pula, fluida awalnya di bagian (1) telah bergerak sejauh 𝜕ℓ1/V1𝜕t , di mana V1 adalah kecepatan fluida di bagian (1). Kita asumsikan fluida mengalir melintasi bagian (1) dan (2) dalam arah normal terhadap permukaan ini dan bahwa V1 dan V2 konstan di seluruh bagian (1) dan (2).
Seperti yang ditunjukkan dalam Gambar 4.11c, aliran keluar dari volume kontrol dari waktu t hingga t + 𝛿𝑡 ditunjukkan sebagai volume II, aliran masuk sebagai volume I, dan volume kontrol itu sendiri sebagai CV. Dengan demikian, sistem pada waktu t terdiri dari fluida di bagian CV; yaitu, "SYS CV" pada waktu t. Pada waktu t + 𝛿𝑡 sistem terdiri dari fluida yang sama yang sekarang mengisi bagian (CV - I) + II. Yaitu, "SYS CV - I + II" pada waktu t + 𝛿𝑡. Volume kontrol tetap sebagai bagian CV untuk semua waktu.
Jika B adalah parameter ekstensif dari sistem, maka nilai B untuk sistem pada waktu t adalah
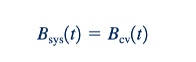
karena sistem dan fluida dalam volume kontrol bersamaan pada waktu ini. Nilainya pada waktu t + 𝛿𝑡 adalah
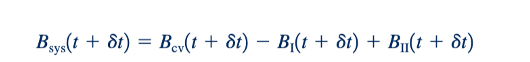
Oleh karena itu, perubahan dalam jumlah B dalam sistem, dBsys, dalam interval waktu Oleh karena itu, perubahan dalam jumlah B dalam sistem, 𝛿Bsys, dalam interval waktu 𝛿𝑡 dibagi oleh interval waktu ini diberikan oleh
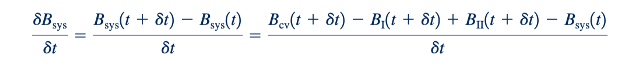
Dengan menggunakan fakta bahwa pada waktu awal t kita memiliki Bsys(t) = Bcv(t), ungkapan yang kurang rapi ini dapat diubah menjadi:
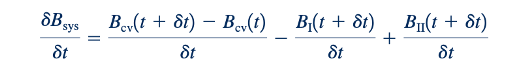
Dalam batas 𝛿𝑡→ 0, bagian kiri Persamaan 4.10 sama dengan laju perubahan waktu dari B untuk sistem dan disebut sebagai DB/dt. Kita menggunakan notasi turunan materi, D()/Dt, untuk menunjukkan laju perubahan waktu ini untuk menekankan karakter Lagrangian dari istilah ini. Ingatlah dari Bagian 4.2.1 bahwa turunan materi, D(P)/Dt, dari suatu kuantitas P mewakili laju perubahan waktu dari kuantitas tersebut yang terkait dengan sebuah partikel fluida yang diberikan saat bergerak. Demikian pula, kuantitas DB/dt_sys mewakili laju perubahan waktu dari sifat B yang terkait dengan sistem (sebuah bagian tertentu dari fluida) saat bergerak. Dalam batas 𝛿𝑡→ 0, istilah pertama di sebelah kanan Persamaan 4.10 terlihat sebagai laju perubahan waktu dari jumlah B dalam volume kontrol
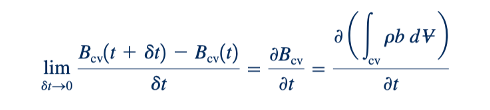
Istilah ketiga di sebelah kanan Persamaan 4.10 mewakili laju di mana parameter ekstensif B mengalir dari volume kontrol melintasi permukaan kontrol. Seperti yang ditunjukkan oleh gambar di sisi margin, selama interval waktu dari t = 0 hingga t = 𝛿𝑡, volume fluida yang mengalir melintasi bagian (2) diberikan oleh δ∀ II = A2𝛿ℓ2 = A2(V2𝛿𝑡). Dengan demikian, jumlah B dalam daerah II, daerah aliran keluar, adalah jumlahnya per unit volume, 𝜌𝑏, dikalikan dengan volume.
dimana b2 dan p2 adalah nilai konstan dari b dan r di seluruh bagian (2). Dengan demikian, laju di mana properti ini mengalir dari volume kontrol, B out , diberikan oleh
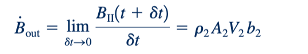
Demikian pula, aliran masuk B ke dalam volume kontrol melintasi bagian (1) selama interval waktu dt sesuai dengan yang ada di daerah I dan diberikan oleh jumlah per unit volume dikalikan dengan volume, δ∀1 = A1 𝛿ℓ1 = A1 (V1𝛿t). Oleh karena itu,
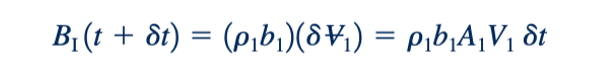
dimana b1 dan p1 adalah nilai konstan dari b dan p di seluruh bagian (1). Dengan demikian, laju aliran masuk properti B ke dalam volume kontrol, Bin , diberikan oleh
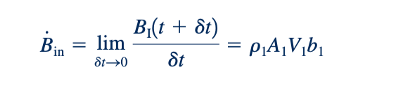
Jika kita menggabungkan Persamaan 4.10, 4.11, 4.12, dan 4.13, kita melihat bahwa hubungan antara laju perubahan waktu dari B untuk sistem dan untuk volume kontrol diberikan oleh
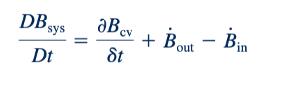
Atau
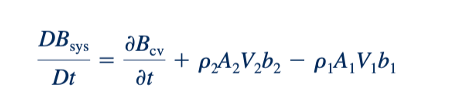
Ini adalah versi teorema transportasi Reynolds yang berlaku di bawah asumsi yang membatasi yang terkait dengan aliran yang ditunjukkan dalam Gambar 4.11—volume kontrol tetap dengan satu masukan dan satu keluaran yang memiliki sifat seragam (kepadatan, kecepatan, dan parameter b) di seluruh masukan dan keluaran dengan kecepatan normal terhadap bagian (1) dan (2). Perhatikan bahwa laju perubahan waktu dari B untuk sistem (bagian kiri dari Persamaan 4.15 atau kuantitas dalam Persamaan 4.8) tidak selalu sama dengan laju perubahan dari B dalam volume kontrol (istilah pertama di sebelah kanan Persamaan 4.15 atau kuantitas dalam Persamaan 4.9). Ini benar karena laju aliran masuk (b1,p1,V1,A1) dan laju aliran keluar (b2, p2, V2, A2) dari properti B untuk volume kontrol tidak perlu sama.

Persamaan 4.15 adalah versi disederhanakan dari teorema transportasi Reynolds. Sekarang kita akan menurunkannya untuk kondisi yang jauh lebih umum. Volume kontrol tetap umum dengan fluida yang mengalir melaluinya ditunjukkan dalam Gambar 4.12. Medan aliran dapat sangat sederhana (seperti dalam pertimbangan aliran satu dimensi di atas), atau itu dapat melibatkan situasi tiga dimensi yang cukup kompleks dan tidak stabil seperti aliran melalui jantung manusia seperti yang diilustrasikan oleh gambar di sisi margin. Dalam setiap kasus, kita lagi-lagi mempertimbangkan sistem sebagai fluida dalam volume kontrol pada waktu awal t. Beberapa waktu kemudian, sebagian dari fluida (daerah II) telah keluar dari volume kontrol, dan fluida tambahan (daerah I, yang bukan bagian dari sistem asli) telah masuk ke dalam volume kontrol.
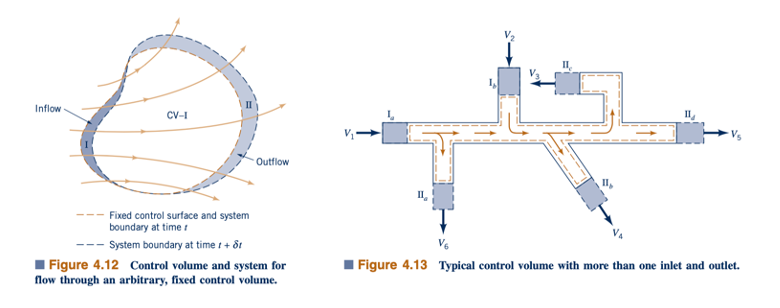
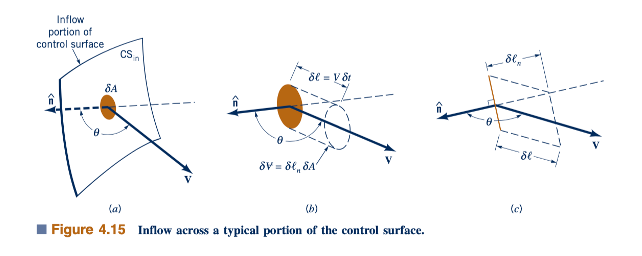
Kita mempertimbangkan sebuah sifat fluida ekstensif B dan mencoba untuk menentukan bagaimana laju perubahan B yang terkait dengan sistem berkaitan dengan laju perubahan B dalam volume kontrol pada setiap saat. Dengan mengulangi langkah-langkah yang sama seperti yang kita lakukan untuk volume kontrol yang disederhanakan yang ditunjukkan dalam Gambar 4.11, kita melihat bahwa Persamaan 4.14 juga berlaku untuk kasus umum, asalkan kita memberikan interpretasi yang tepat untuk istilah-istilah B out dan B in. Secara umum, volume kontrol mungkin mengandung lebih (atau kurang) lebih dari satu masukan dan satu keluaran. Sistem pipa yang khas dapat mengandung beberapa masukan dan keluaran seperti yang ditunjukkan dalam Gambar 4.13. Dalam kasus seperti itu, kita berpikir bahwa semua masukan dikelompokkan bersama-sama (I= Ia + Ib + Ic +I. . . .) dan semua keluaran dikelompokkan bersama-sama (II = IIa+ IIb +IIc +II. . . .) , setidaknya secara konseptual. Istilah Bout mewakili laju aliran bersih dari properti B dari volume kontrol. Nilainya dapat dianggap berasal dari penjumlahan (integrasi) kontribusi melalui setiap elemen area infinitesimal berukuran 𝛿A pada bagian permukaan kontrol yang memisahkan daerah II dan volume kontrol. Permukaan ini ditandai sebagai CSout. Seperti yang ditunjukkan dalam Gambar 4.14, dalam waktu 𝛿ℓt, volume fluida yang melewati setiap elemen area diberikan oleh δ∀= 𝛿ℓn 𝛿A, di mana 𝛿ℓn = 𝛿ℓ cosθ adalah tinggi (normal terhadap dasar, δA) dari elemen volume kecil, dan θ adalah sudut antara vektor kecepatan dan normal ke permukaan, n. Dengan demikian, karena 𝛿ℓn=V𝛿t, jumlah properti B yang dibawa melintasi elemen area 𝛿A dalam interval waktu 𝛿t diberikan oleh
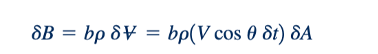
Laju di mana B dibawa keluar dari volume kontrol melintasi elemen area kecil 𝛿A, yang ditunjukkan sebagai 𝛿Bout, adalah
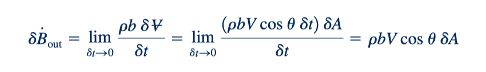
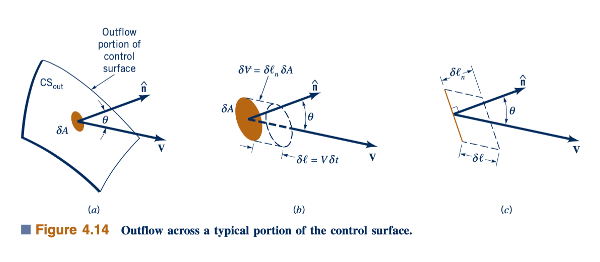
Dengan mengintegrasikan di seluruh bagian aliran keluar dari permukaan kontrol, CSout, kita memperoleh
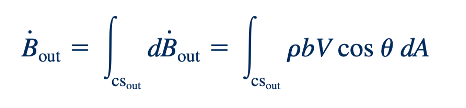
Kuantitas V cos θ adalah komponen kecepatan yang normal terhadap elemen area 𝛿A. Dari definisi dari produk dot, ini dapat ditulis sebagai V cos θ=V⋅n. Oleh karena itu, bentuk alternatif dari laju aliran keluar adalah
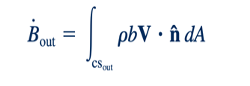
Secara serupa, dengan mempertimbangkan bagian aliran masuk dari permukaan kontrol, CSin, seperti yang ditunjukkan dalam Gambar 4.15, kita menemukan bahwa laju aliran masuk B ke dalam volume kontrol adalah
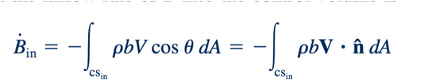
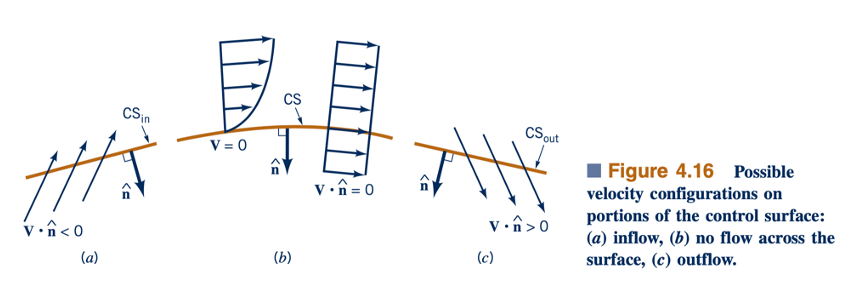
Kita menggunakan notasi standar bahwa vektor normal satuan terhadap permukaan kontrol, n, menunjuk keluar dari volume kontrol. Dengan demikian, seperti yang ditunjukkan dalam Gambar 4.16, 90°≤ θ≤ 90° untuk daerah aliran keluar (komponen normal dari V positif; V⋅n>0). Untuk daerah aliran masuk 90°≤ θ ≤ 270° (komponen normal dari V negatif; V⋅n<0). Nilai dari cosθ oleh karena itu positif pada bagian CVout dari permukaan kontrol dan negatif pada bagian CVin. Di atas sisa permukaan kontrol, tidak ada aliran masuk atau aliran keluar, menghasilkan V⋅n⋅cosθ=0 pada bagian-bagian tersebut. Pada bagian-bagian seperti itu, baik V=0 (fluida "menempel" pada permukaan) atau cosθ=0 (fluida "meluncur" di sepanjang permukaan tanpa melintasinya) 1lihat Gambar 4.1622. Oleh karena itu, aliran bersih B di seluruh permukaan kontrol adalah
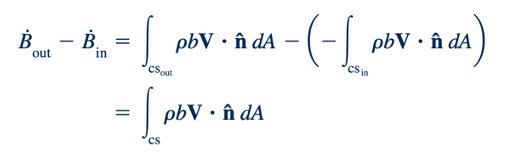
dimana integrasi dilakukan melintasi seluruh permukaan kontrol.
Dengan menggabungkan Persamaan 4.14 dan 4.18, kita mendapatkan
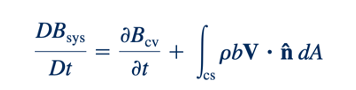
Ini dapat ditulis dalam bentuk yang sedikit berbeda dengan menggunakan Bcv ≈ ∫CV pb d∀ sehingga